Recurrent Neural Network Based Hybrid Model of Gene Regulatory Network
- 杂志: Computational biology and chemistry
- IF: 1.581
- 分区: 4区
Introduction
建模生物网络的目的:
- 网络的模式可以提供更好的、在整体上的、关于交互和关联的理解;
- 允许研究者对gene的功能进行预测并验证;
- 分子和细胞间交互作用的复杂性,使得我们也对这种能够设计和解释实验结果的建模工具有着巨大的需求;
- 对于理解细胞行为是关键的,可能会启发更好的治疗方法;
- 可以预测更多的未知的生物大分子;
- 可以为药效模拟提供依据。
基因调控网络(gene regulatory networks, GRNs)
- 包括了输入信号通路、接受输入信号的调控蛋白、靶基因、靶基因产生的RNA和蛋白质等。
- 可能还有动态的反馈调节。
- 使用graph的形式来表示,其中node是genes,edge是调控关系。是一个directed graph。
本研究提出了一种hybrid方法,基于RNN,并整合了generalized extended Kalman filter。
建模GRNs的方法
文章中列举了很多,这里就只把其分类说一下就好了
- Directed Graph
- Boolean networks
- Bayesian networks
- linear and non-linear ordinary differential equations(ODEs)
- machine Learning approaches
之后介绍的大多数方法都是基于ML的了,而且大多数是基于NNs的了
- 【Vohradsky, 2001】使用ANN来进行建模,但模型参数过多;
- 【Keedwell et al., 2002】简化了上述模型,并且使用标准的BP算法来进行学习;
- 【Tian & Burrage, 2003】使用了随机神经网络来建模GRNs;
- 【Xu et al., 2004】则使用RNN来进行建模,使用BPTT和PSO(粒子群算法)来进行学习;
- 【Chiang & Chao, 2007】将GA和RNN杂交(GA-RNN)去进行学习;
- 【Xu et al, 2007b】提出了PSO-RNN;
- 【Xu et al., 2007a】进一步去试验了另外的3种优化方法:DE、PSO、DE-PSO,发现DE-PSO和RNN的结合是最好的;
- 【Ghazikhani et al., 2011】提出了一个基于multi-population PSO算法的模型,在SOS repair network的构建中体现除了更好的效果;
- 【Noman et al., 2013】提出了decoupled-RNN model,decoupled意味着其将参数的估计分成几部分进行,从而提高了效率,使得对于大规模网络的建模称为可能;
- 【Raza et al., 2014】,这是作者的早期研究,使用了一种进化算法-ACO来找到genes间的关键交互。
Methods
RNNs
这一部分涉及RNNs基础的,就不再赘述了。
从后面对于模型的叙述并结合这一部分的RNNs的介绍,这里的RNNs并不是DL中的RNNs,而更像是前DL时代中的RNNs
基于RNNs的GRNs模型
假设:特定基因上的调控效应可以表示为NN的形式,其中节点表示的是gene,链接表示的是调控关系。
根据【Rui et al., 2004; Hu et al., 2005; Noman et al., 2013; Raza, 2014】,GRNs的模型可以表示为以下的格式:
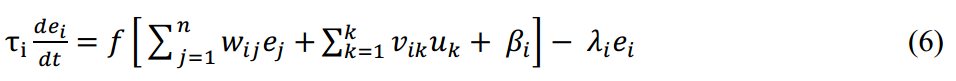
其中\(e_i\)表示基因\(i\)的表达水平,\(n\)表示所有的genes的数量,\(f\)是一个非线性函数,一般使用sigmoid(\(f(z)=1/(1+exp(-z))\)),\(w_{ij}\)表示gene \(j\)对gene \(i\)的调控权重。\(u_k\)表示的是外部变量,\(v_{ik}\)表示的是外部变量对gene \(i\)的影响。\(\tau_i\)是一个时间常数,\(\beta_i\)是偏置项,\(\lambda_i\)是衰减率参数。
我们可以知道,\(w_{ij}\lt0\)表示gene \(j\)对gene \(i\)是抑制作用,而\(w_{ij}=0\)表示gene \(j\)对gene \(i\)没有调控作用。
上面公式也可以写成下面的离散形式:
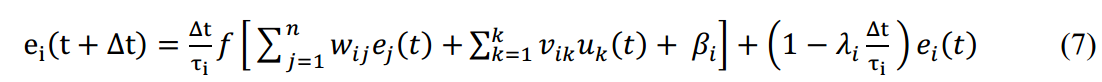
使用BPTT来训练
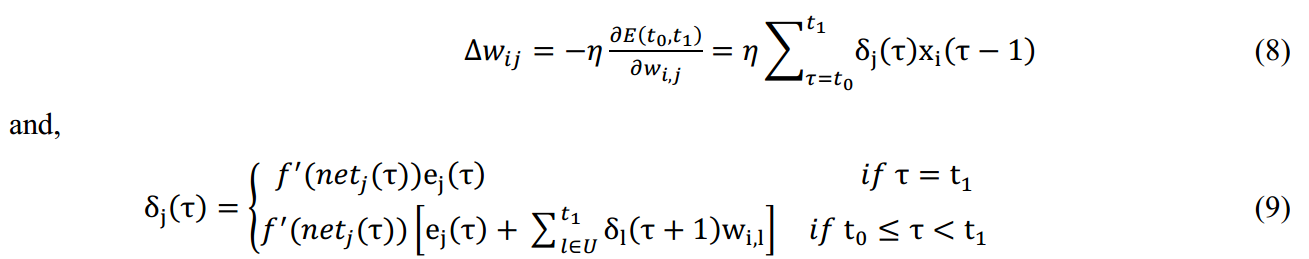
Kalman filter
关于卡尔曼滤波器的基本信息,可以查看wiki。
这里是一个关于kalman filter的解释,可能更加容易理解。
一个时间序列,我们已知一个时间点\(t\)的最佳估计(当然这个估计也是随机的,有一个方差),我们有两种方式来得到下一个时间点\(t+1\)的估计:
- 根据时间点间的关系进行预测、
- 直接在下一个时间点进行测量或观测。
但还有一个更好的方式,就是将这两种方式结合,此即卡尔曼滤波。
简单来说,就是通过计算预测和观测各自的方差,利用方差做权重来调整对下一个时间点的估计。如果利用贝叶斯的观点来说,预测得到的结果可以看做是下一个时间点的先验估计,而观测可以看做是样本,然后调整先验估计,得到后验估计。
在kalman filter的命名中,预测即predict,而观测进行调整的过程即correct。
如果上一个时间点的估计是精确的,即此时方差为0,则计算权重的时候将不会再为观测分配权重,则整个时间序列过程退化为一个确定性过程。
更加general的模型还会有一个外部环境影响因素,这个也是一个随机变量,则此时,就算是初始估计是精确地,因为此随机外部环境的影响,我们也无法忽略观测过程。
在本文的例子中,RNN所预测的权重被看做是一个预测。
对于本文用到的generalized extended kalman filter (GEKF),是更加general的清楚,将非线性的过程加入其中。

如何把RNN的weight matrix应用到Kalman filter中进行处理,这一段没有看懂???
工作流程
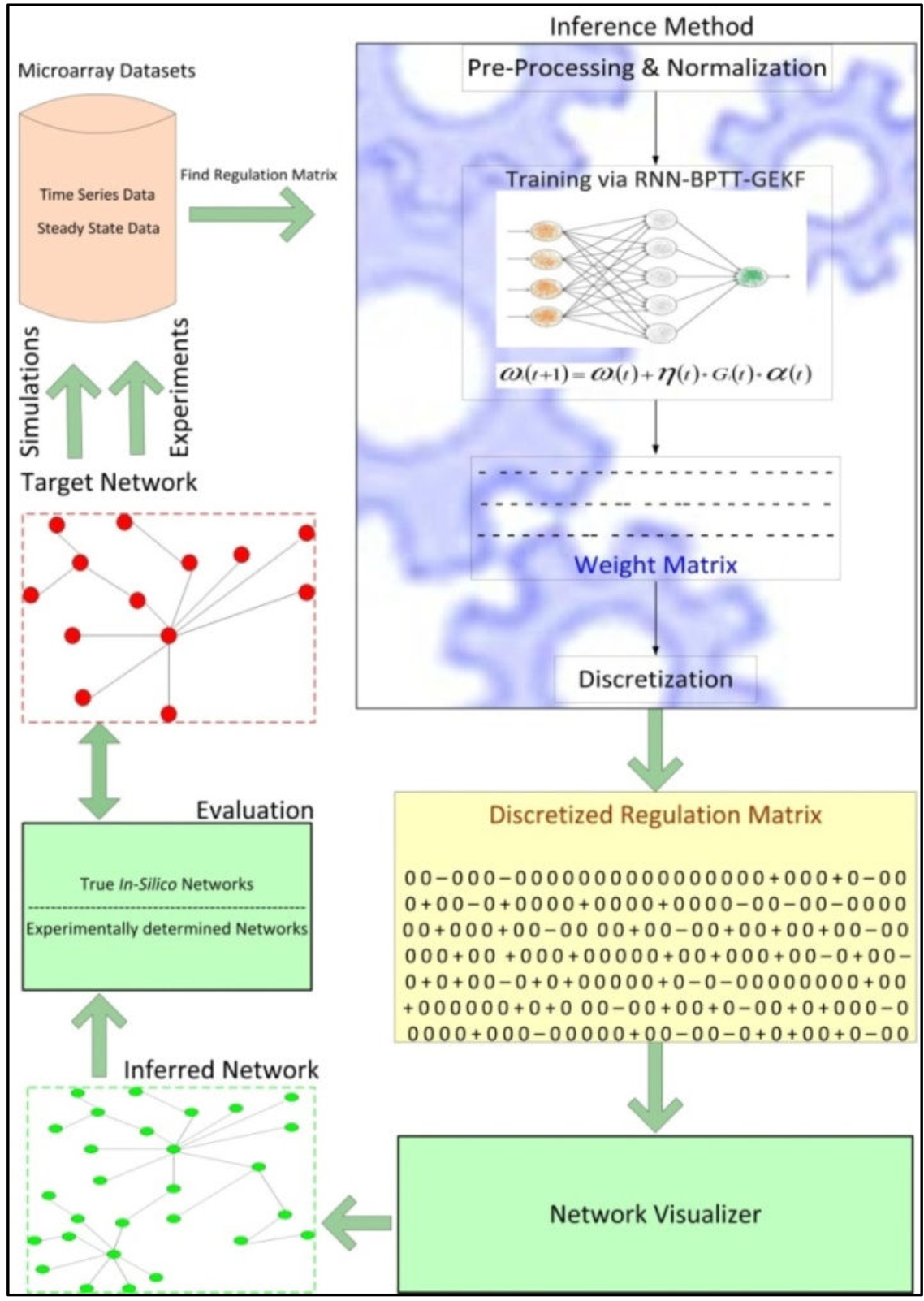
- 读取microarray数据(时间序列数据或者稳态数据),并进行预处理和标准化;
- 模型训练;
- 读取模型的weight matrix,将其离散化为0和1;
- 将离散化的matrix可视化;
- 和true network进行比对,对结果进行评价。
Results and Discussion
本方法一共在4个数据集(2个real、2个simulated)上进行了验证和比较。
SOS DNA repair networks
使用proposed method得到weight matrix,然后应用Inter-Quartile离散化,得到结果如下:

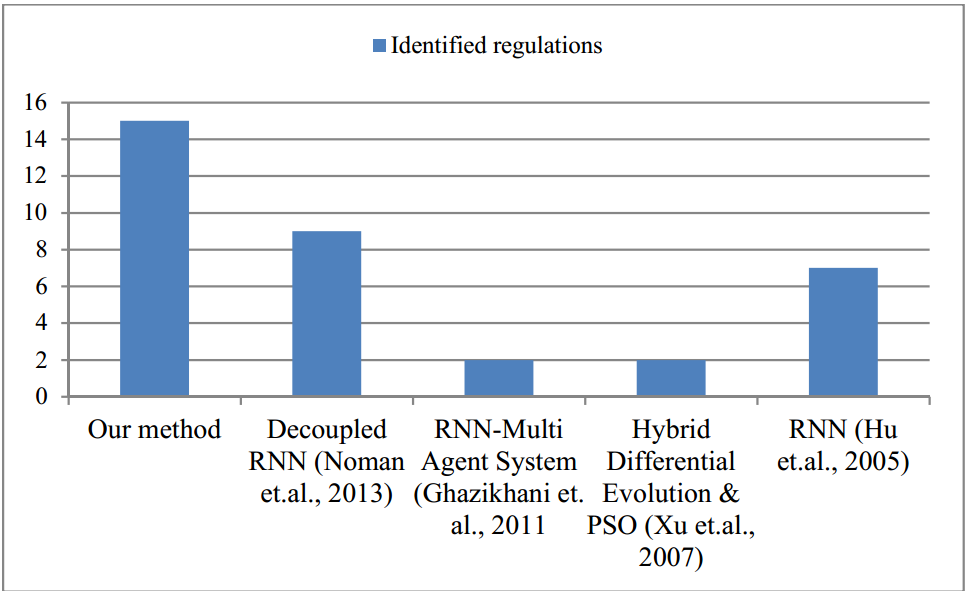
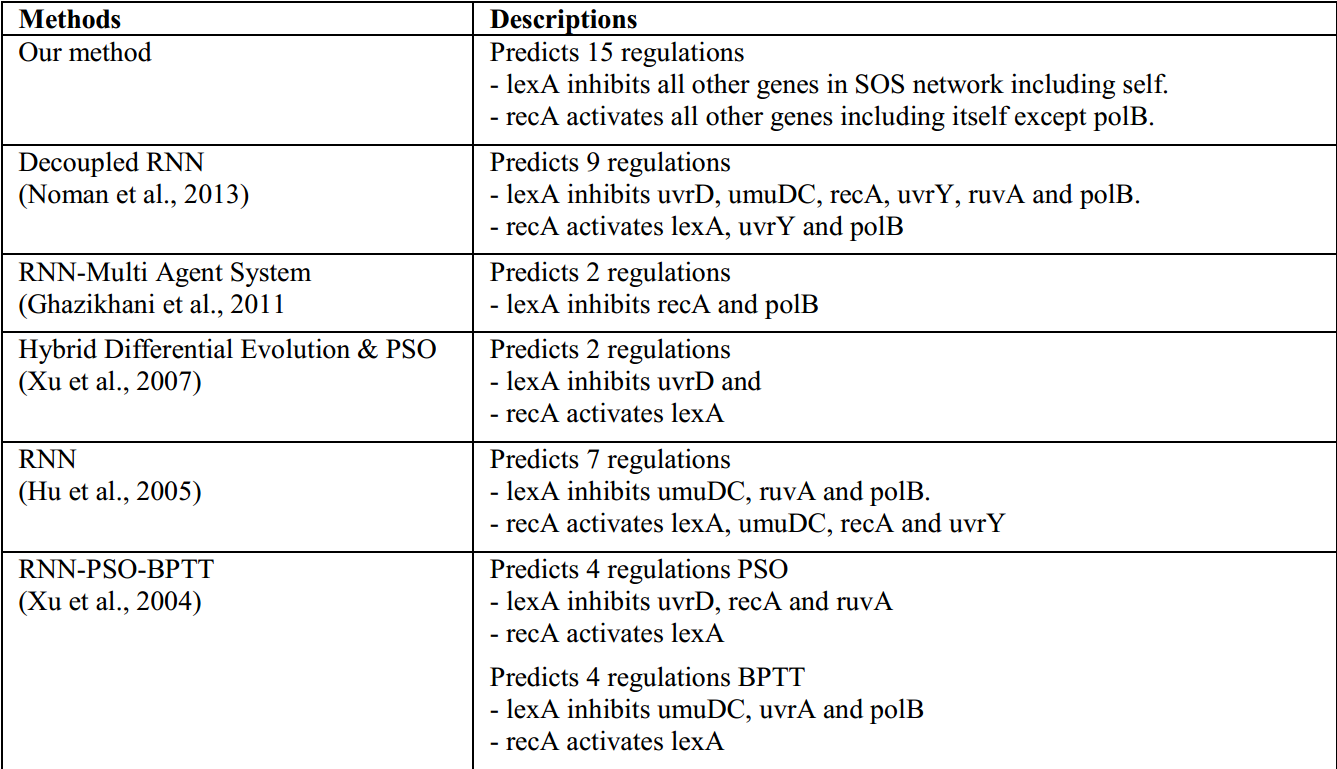
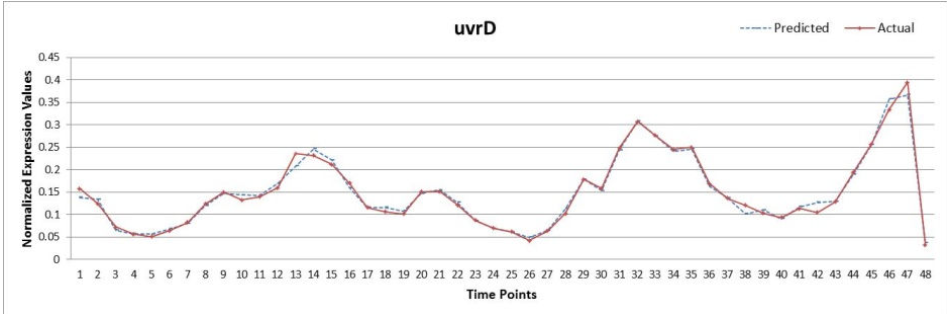
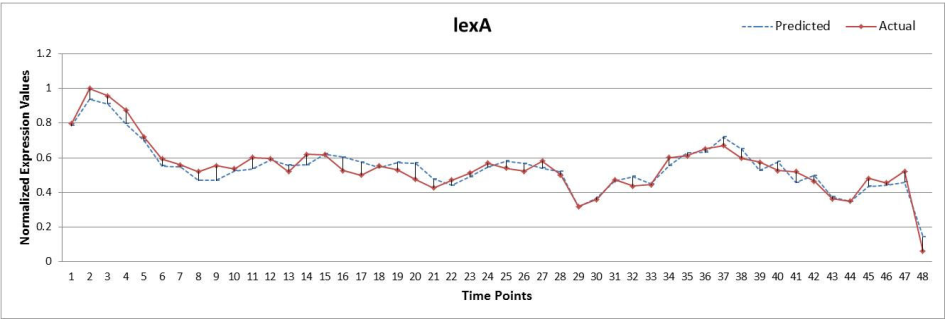
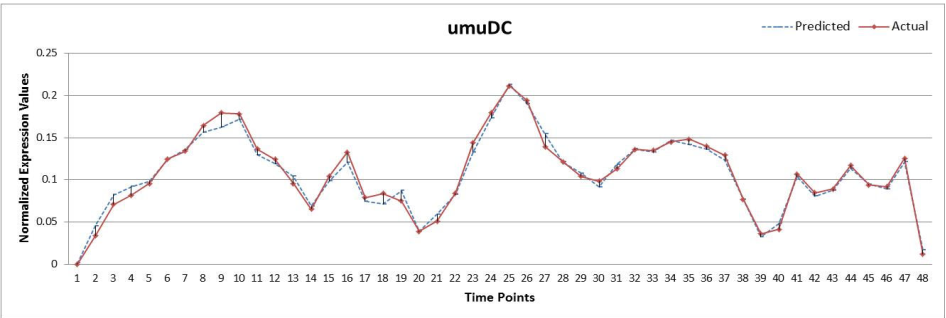
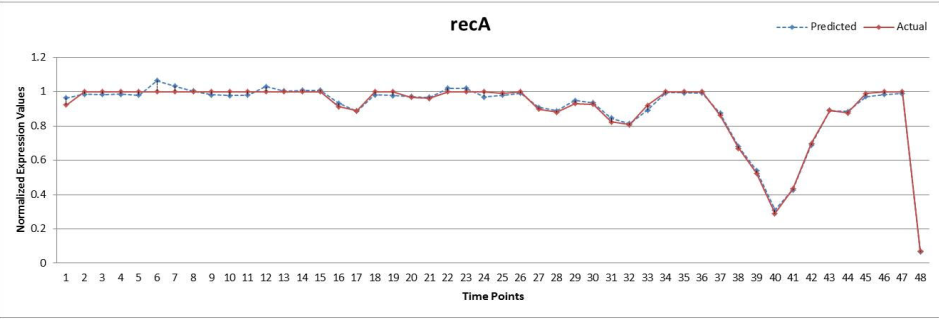
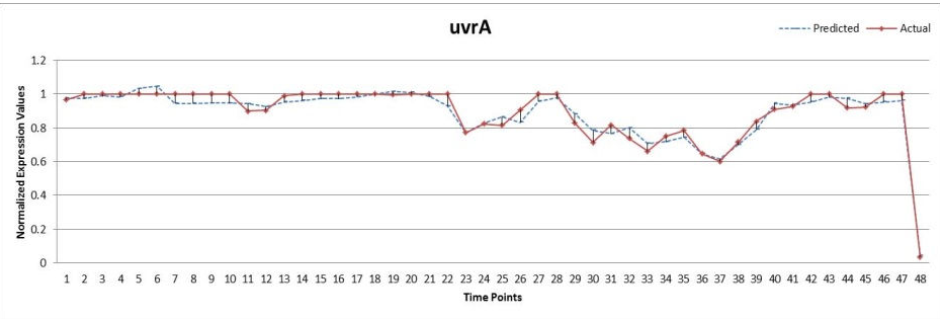
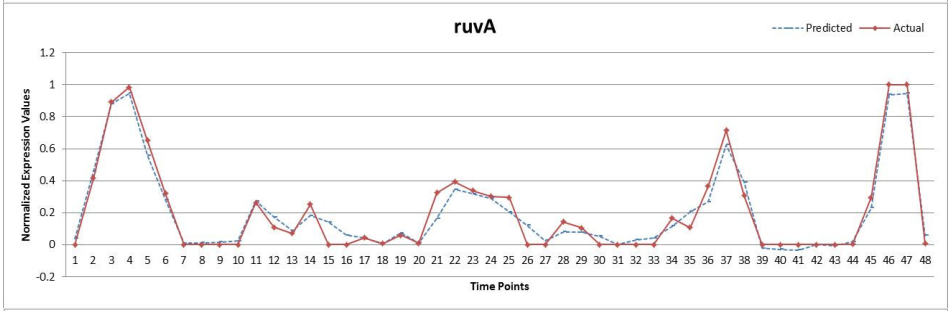
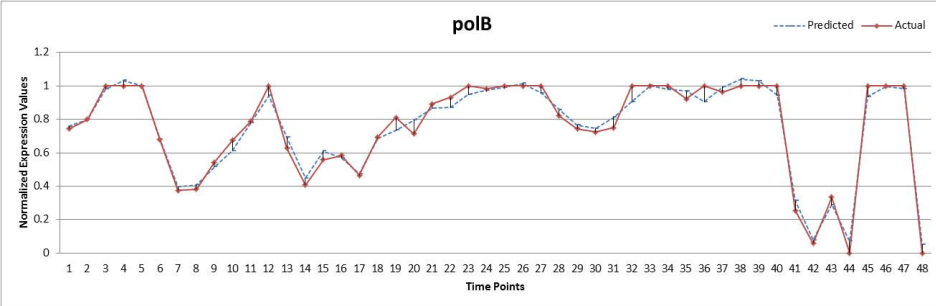
in-vivo reverse-engineering and assessment yeast network (IRMA)
switch OFF状态
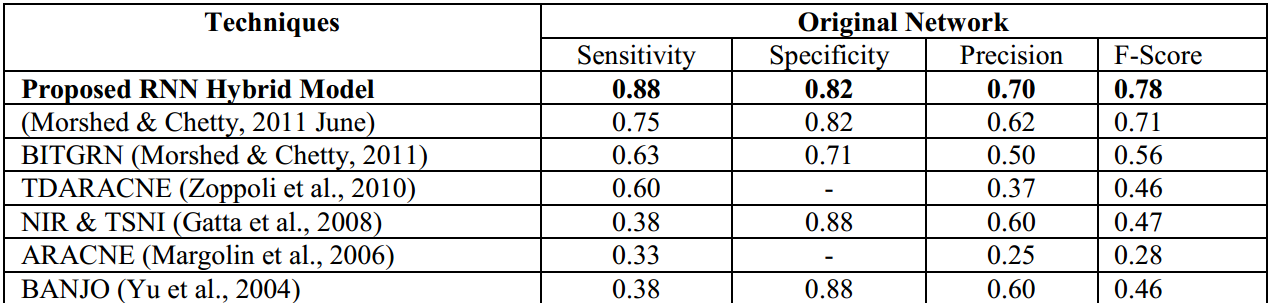
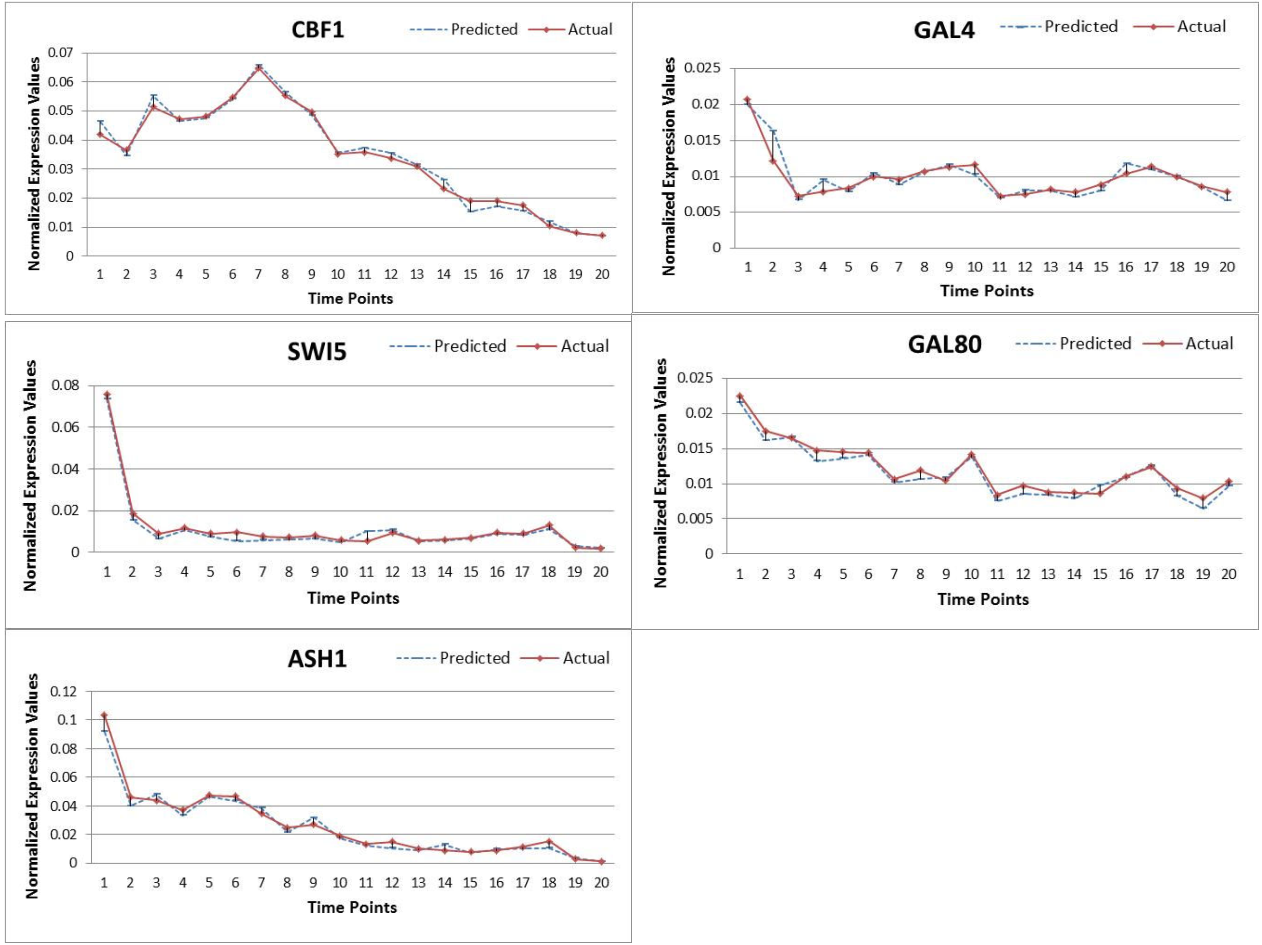
swith ON状态
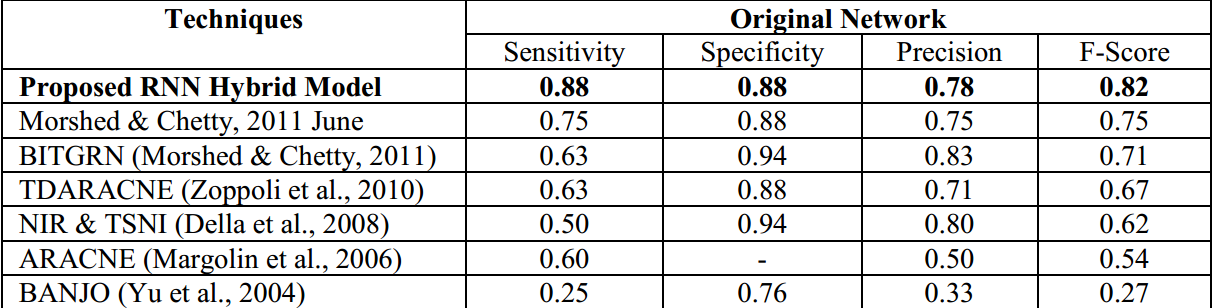
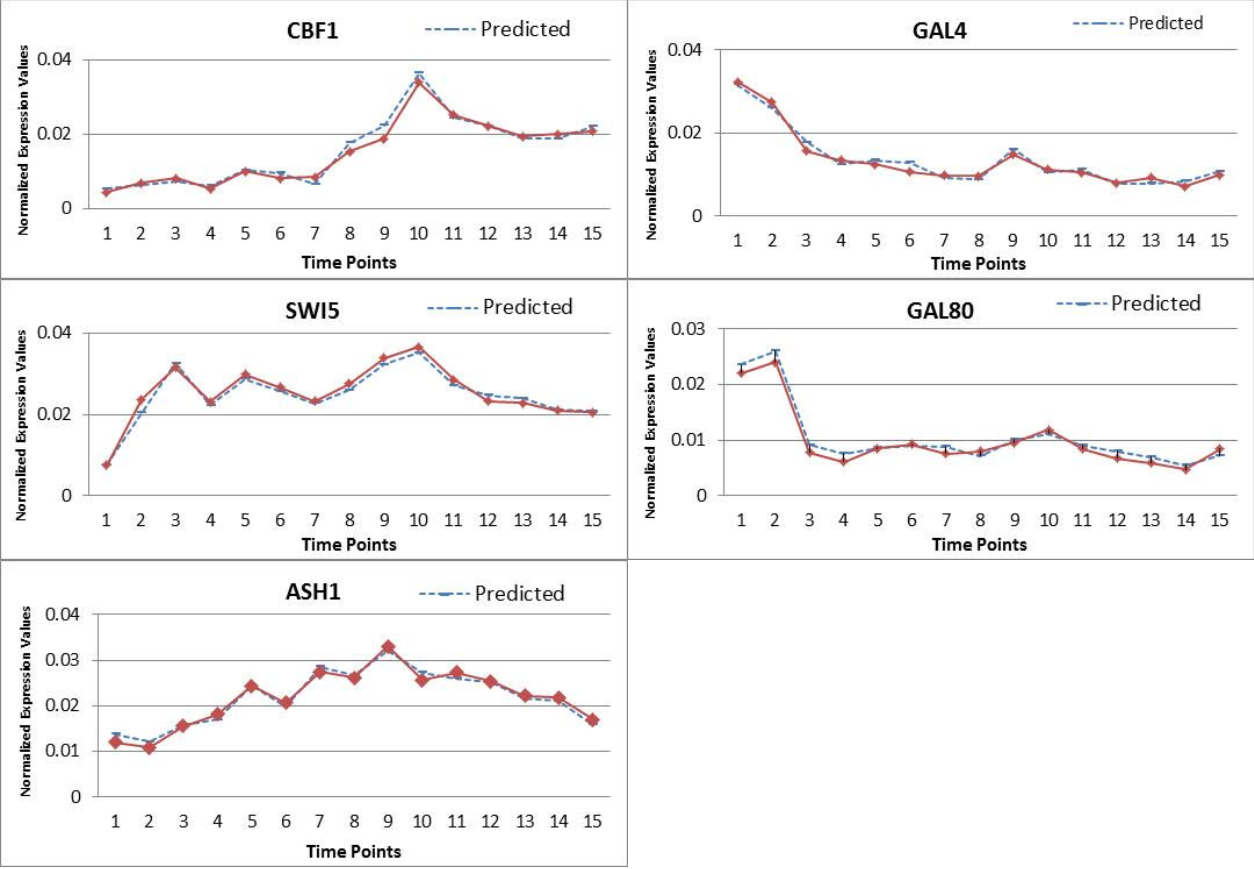
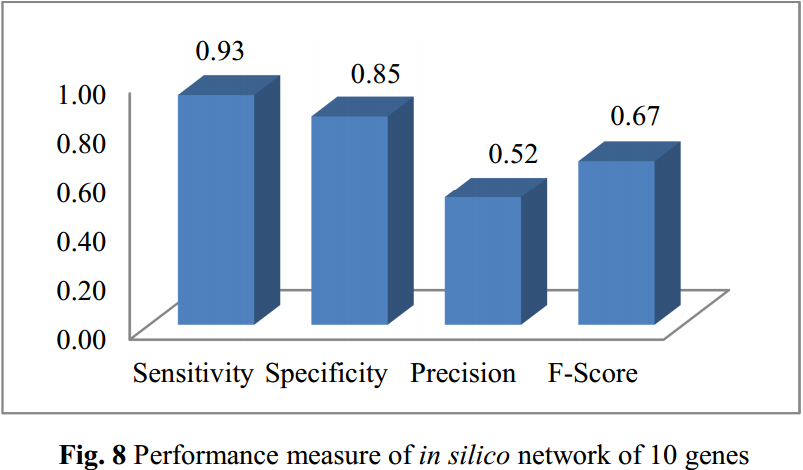
silico networks(simulated data,DREAM4)
DREAM4 10-genes network:
DREAM3 50-genes network:
一共125条调控作用,预测到其中的121条,但有662条假阳性预测,得到了0.76的sensitivity和0.72的specificity。
模型的稳健性
在silico 10-genes data上加了5% std的高斯噪声,发现proposed method还是能够得到不错的预测:
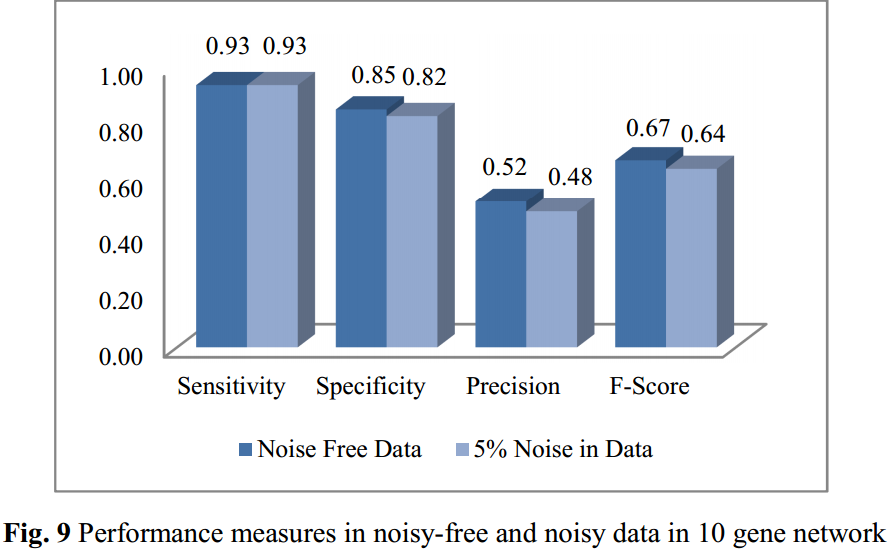
Conclusion
本文提出了一种基于RNN的基因调控网络构建方法,其混合使用Kalman filter对weight matrix进行进一步的增强。在4个数据集上进行了验证,发现在前3个数据集上都能够超越之前的建网方法。另外,还进行了稳健性的验证,也得到了不错的结果。
基因调控网络的构建依然面临着诸多问题:维度灾难问题、数据的异质性(比如批次)噪声、不可靠数据等,有待进一步解决。
Questions
读过本文后才发现,本文并不是deep learning意义上的RNNs的应用,这里RNNs的定义还带有前DL时代的影子。这里的RNNs只是单层的,其应用的目的也只是为了解决一个普通的时间序列预测问题。
在我看来,本文的主要贡献是在于在RNNs之后又应用了kalman filter进行进一步的校正。这样的组合让我想起了我研究生期间研究的一种建网策略:即先利用建网方法进行网络建立,然后使用一些方法来删除其中的假阳性预测。我想这两者之间在策略、哲学上还是有共同之处的。
通过阅读本论文,我第一次、一定程度地了解了Kalman filte的知识,希望在之后的研究中有帮助吧。
但本研究对于RNN和filter的组合太过生硬了,而且实验使用的数据集gene的数量也不多,还没有到达组学的范畴。
本文所叙述的一些内容(使用的数据集,kalman filter等)我是第一次接触,所以读起来还是有些磕磕绊绊,results部分也是简单的浏览了一下表格和图,没有进行深入的理解。
下面的是我在阅读时产生的问题,权当是为了记录而记录,便于当之后的研究需要本文时有个快速回忆的锚点。
- 在这个kalman filter过程中,什么充当了观测的角色?



