论文精读-VAE-2013

Auto-Encoding Variational Bayes

• 杂志: None
• IF: None
• 分区: None
• github

---

Introduction

1. 对带有连续隐变量的概率图模型进行概率密度估计时，会存在一个难以处理的后验分布。variational bayesian（VB，或者叫做variational inference（VI），其最常见的实现是mean-field方法）可以进行近似推断。但现有的技术存在一些问题：

   • 类似mean-field的方法需要小心地选择使用的函数，使得变分下界（variational lower bound，或者evidence lower bound，ELBO）有精确解。
   • 使用Monte Carlo方法来估计ELBO或ELBO的梯度（ELBO本质上是一个期望）可以避免精确解的需求，但现有的方法的估计方差比较大，使得后验估计或随之而来的参数学习过程无法有效的完成。

2. 本研究介绍了一种基于recognition model的Monte Carlo方法来进行后验估计，称为SGVB。其将ELBO参数化，并通过重参数化技巧降低了Monte Carlo估计的方差，可以使用随机梯度下降算法进行训练。

   这实际上就是概率图模型的inference

3. 更进一步，将信息编码理论（自编码器）和SGVB结合，本研究进一步提出了AEVB算法。其可以利用SGVB的后验估计能力进行概率图模型的参数学习，比iterative inference方法（如MCMC）更加有效率，得到的模型可以用于识别、去噪、表示、可视化等多种任务。

   这里指的实际上是概率图模型的learning

   当AEVB方法是使用神经网络（NN）实现时，即我们熟知的variational autoencoder（VAE）算法。

为了能够对本文有更好的认识，需要以下的背景知识

1. 先验和后验分布

在bayes统计中，有先验和后验的概念：

\[p(H=h|X) = \frac{p(X|H=h)p(H=h)}{\int{p(X|H=s)p(H=s)}ds} \tag{1}\]

其中\(p(H|X)\)为后验分布（posterior），\(p(H)\)为先验分布（prior），\(p(X|H)\)为似然函数（likelihood），如果是有多个iid样本的话，其一般表示为\(\prod_{i=1}^N{p(X=x_i|H)}\)，分母的部分被称为证据（evidence）。bayes统计的关键在于如何在已知先验、似然函数的基础上来得到后验，计算方式就来自上面的公式。但在以上计算式中，分母通常难以得到：

• 对于高维的\(H\)，我们无法通过近似离散方法得到。
• 而对于比较复杂的似然函数和先验分布形式，我们也无法得到精确解（甚至有时候似然函数和先验分布的精确形式也无法得到）。

所以必须使用一些inference的方法来进行推断。

2. 隐变量模型

典型的隐变量模型有：GMM（高斯混合模型）、HMM（隐马尔可夫）等。通常隐变量模型可以看做是一个有向图模型，其中箭头由隐变量指向显变量表示了数据的生成方式。

我们有显变量\(X\)，其分布依赖于一些隐变量\(H\)，由隐变量得到显变量的关系式为\(p(X|H)\)，如果这个关系式未知，则需要使用参数化的函数\(p_{\theta}(X|H)\)来表示，并且需要学习到这个参数\(\theta\)。如果套用图概率模型的概念，则我们一般需要做两个任务：

• inference：已知\(X=x_i\)，其对应的隐变量的分布是什么：\(p(H|X=x_i)\)。

• learning：寻找参数\(\theta^{\star}\)，使得满足下面的边际似然最大化：

  \[\theta^{\star}=\arg\min_{\theta}{\log{p_{\theta}(X)}} \tag{2}\]

显然，对于inference，和bayes统计中的问题是一致的：隐变量分布即\(H\)，显变量即\(X\)，\(p(X|H)\)即似然。

至于learning，在解决了inference后，一般也比较容易解决，毕竟边际似然可以比较容易地由后验来表示：

\[\log{p_{\theta}(X)} = \log{p_{\theta}(X|H)}+\log{p(H)}-\log{p_{\theta}(H|X)} \tag{3}\]

后面我们会看到，使用VI，inference和learning将会走到相同的思路上去，我们同时解决了这两个问题。

当然，有很多模型设计的时候就尽量让模型的训练不依赖于后验估计，这是因为后验估计本身很难，所以其learning的算法和后验估计是没有关系的。

3. MCMC

MCMC是进行后验推断的最重要的方法，特别是在bayes统计领域（MCMC拯救了bayes估计）。

为什么MCMC能够进行进行后验估计？我们需要先简单了解一下MCMC的过程（这里是最简单的Metropolis算法，Metropolis-Hastings算法和他类似，另外的算法也都跑不出其框架）:

target distribution：\(p(X)\)
proposed distribution：\(q(X)\)，任意分布

第一步：随机一个初始值\(X=x_0\)，只要让\(p(X=x_0)\ne0\)即可。

第二步：使用\(q(X)\)得到一个随机的点\(x'_i\)。

第三步：计算transition probability：

\[p_{move}=\min(\frac{p(x'_i)}{p(x_i)}, 1) \tag{4}\] 其中\(p(x_i)\)是当前所在的点。依据此概率来判断是否接受\(x'_i\)作为\(x_{i+1}\)，否则\(x_{i+1}=x_{i}\)。

回到第二步。

现在我们的目标分布是\(p(H|X)\)，当把它代入上面的transition probability的计算的时候，我们发现，分母上的积分式被约掉了，我们只需要能够计算似然和先验就可以进行MCMC采样了。

这也就是为什么MCMC可以进行后验推断的原因。

现实应用的时候，Metropolis或Metropolis-Hastings算法效率非常低，需要使用Gibbs算法或Hamilton算法来替代，但本质上原理是一样的。

MCMC的优点：

• 无偏估计
• 适用性强，只要能够写出似然函数即可

MCMC的缺点：

• 太慢了
• 采集的样本也不能直接用，必须要做一些处理，比如降低其自相关性、预烧期等等，而这些处理并不是容易

4. 变分推断

后验推断的另一种思路，是使用一个可学习的参数化分布（\(q_{\phi}(H)\)）去逼近后验分布。这里使用KL散度来度量两个分布间的相似程度。

由上面的公式\((2)\)，我们可以得到：

\[\log{p(X)} = \log{\frac{p(X|H)}{q_{\phi}(H)}}+\log{p(H)}-\log{\frac{p(H|X)}{q_{\phi}(H)}}\]

等式两边对\(q_{\phi}(H)\)做期望，得到：

\[ \begin{aligned} \log{p(X)}&=-D_{KL}(q_{\phi}(H)|p(X|H))+E_{q_{\phi}}[\log{p(H)}]+D_{KL}(q_{\phi}(H)|p(H|X)) \\ &=\mathbb{E}_{q_{\phi}}[\log{p(X,H)}-\log{q_{\phi}(H)}]+D_{KL}(q_{\phi}(H)|p(H|X)) \end{aligned}\tag{5} \]

等式左边是关于\(\phi\)不变的，所以如果希望最小化\(D_{KL}(q_{\phi}(H)|p(H|X))\)，只需要最大化下面的东西即可，这个就是ELBO(evidence lower bound)：

\[ \begin{aligned} ELBO&=-D_{KL}(q_{\phi}(H)|p(X|H))+E_{q_{\phi}}[\log{p(H)}] \\ &=\mathbb{E}_{q_{\phi}}[\log{p(X,H)}-\log{q_{\phi}(H)}] \end{aligned} \tag{6} \]

以上结果也可以通过Jessen不等式得到
另外，还有研究从weighted sampling的角度来理解VAE，同样可以推导出上面的结果

现在问题就变成了如何最小化ELBO，这时候，\(q_{\phi}(H)\)的选择就变得格外重要了，其必须要满足以下两个方面：

• 足够简单，可以保证ELBO可以计算出来

  注意到，ELBO本质上是一个期望，所以可以使用Monte Carlo方法来估计从而避免显式的去求期望，但此时需要可以对\(q_{\phi}(H)\)采样。

• 足够复杂，能够比较好的拟合后验分布。

这时候，大家传统的选择是mean-field，即使用相互独立的多个分布组成的高维分布来做\(q_{\phi}(H)\)。

5. 平均场

关于mean-field的详细公式推导这里就不写了，之后会辟出单独的篇章来讨论。

在保证了似然函数是简单的（指数分布簇）的前提下，我们可以使用多个相互独立的低维分布组成的高维分布作为\(q_{\phi}(H)\)，这有下面的优点：

• 可以构造很高维的分布，对于高维的\(H\)也可以完成拟合。
• 尽管每个独立的组分是简单的，但只要其是参数化的，其组合而成的高维分布依然是有一定的拟合能力的。
• 只要每个组分是简单的（指数族分布），那么不管有多少个组分，都可以迭代的、显式的将ELBO计算出来，从而完成inference。
• 显式的计算出ELBO，意味着没有使用Monte Carlo估计，自然其相关的缺点也没有（估计有误差等等）。

但是其缺点也是显然的：

• 显然\(q_{\phi}(H)\)能够拟合的函数的范围也非常有限。
• 要求似然函数比较简单，容易计算，这在很多模型中无法办到。

本文使用Monte Carlo估计的方法来克服上述缺点，并且尽量规避了Monte Carlo估计自身所带来的缺点

Methods

1. 问题

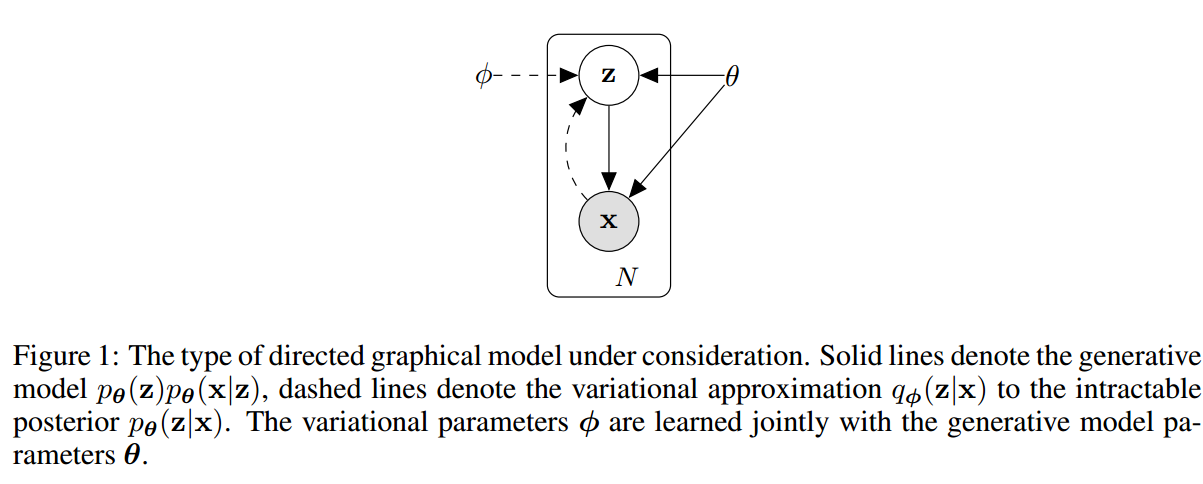
现在将讨论的范围限制在下面的区域内（如上图所示的模型）：

数据集为\(X=\{x^{(i)}\}_{i=1}^N\)，是iid的，假设数据由某个未观测到的连续变量\(z\)生成，其有两个步骤：

1. \(z\)从某个先验的分布\(p_{\theta}(z)\)得到；
2. \(x^{(i)}\)由条件概率\(p_{\theta}(x|z)\)得到。

另外假设这两个分布都是可以参数化的（\(\theta\)），而且对于参数是可导的。在此之外，不再增加额外的假设。

假设这些分布可以由NN参数化，则就使用NN构建模型；假设这些分布可以由线性模型参数化，则使用线性函数构建模型......

现在，我们希望构建一个模型，得到下面的结果：

1. 每个iid样本都有一个对应的隐变量；
2. 使用maximum likelihood（ML，实际上最大化的是边际似然）和 maximum a posteriori（MAP）来估计参数\(\theta\)；
3. 使用变分推断来估计隐变量。

我们会面临两个问题：

• Intractability：边际似然\(p(X)\)不好算、后验分布不好算、似然函数很复杂（比如是一个NN）导致传统的mean-field用不了。
• large dataset：大数据，所以batch optimization无法做到，凡是基于采样的方法也无法做到。

我们希望得到的解决方法具有下面的特点：

• 能够进行高效地ML或MAP，估计\(\theta\)，从而model可以进行数据生成；
• 能够高效地估计给定\(x\)的后验分布\(z\)，从而可以对数据进行编码或表示学习；
• 能够得到\(x\)的边际估计，从而可以进行降噪、补全或超分辨率操作。

为了能够得到上面的特性，这里引入一个recognition model\(q_{\phi}(z^{(i)}|x^{(i)})\)，来逼近真实后验。需要注意到，这里的\(q_{\phi}(z^{(i)}|x^{(i)})\)不需要有mean-field的独立性假设和closed-form expectation，比如可以是一个NN。

注意到现在我们是希望为每个样本求各自的后验分布。

如果熟悉贝叶斯统计可能知道，为每个对象或单位都搞一个后验，一般出现在层次模型中（Hierarchical Models）：

一个人\(n\)的血压服从一个分布\(x^i_n\sim p(x^i_n|x_n)\)，比如是gaussian。自然这个分布有参数--个人的血压平均值\(x_n\)，其服从另一个分布--所有人的血压平均值分布\(x_n\sim p(x_n|x)\)（假设其还是服从一个gaussian）。这个分布依然有一个参数（可以看做是全世界人的血压平均值），这个参数服从一个先验分布\(x\sim p(x)\)。

这里就要涉及到关于贝叶斯估计的一个问题：显然我们可以将“分布的参数的分布”这个过程无限套娃下去，那到底套娃多少次呢？

这个问题的关键在于我们的任务想要回答什么的问题。

• 一般来说，对于上面的血压的例子，我们希望知道所有人的血压平均值的分布\(x\)的信息，则先验分布最多就设置到它的分布即可。所以上面的例子我们讨论到了\(x\sim p(x)\)。 \[x^i_n\sim p(x^i_n|x_n) \quad x_n\sim p(x_n|x) \quad x\sim p(x)\] 以下是我们想要得到的后验： \[x\sim p(x|\{x^i_n|i\in I_n,n\in N\})\] 其中\(I_n\)和\(N\)表示第n个人的样本指标集合和所有人的指标集合。
• 但有时候，我们希望得到的只是每个人的血压平均值的分布\(x_n\sim p(x_n)\)，则我们就把先验设置到此为止就好了。这时候可以为每个人的血压平均值分布设置相同的先验，也可以为每个人设置不同的先验。此时我们的模型是这样的： \[x_n^i\sim p(x_n^i|x_n) \quad x_n\sim p(x_n)\] 或者 \[x_n^i\sim p(x_n^i|x_n) \quad x_n\sim p_n(x_n)\] 我们得到的后验是： \[x_n\sim p(x_n|\{x_n^i|i\in I_n,n\in N\})\] 如果进一步假设各个人间是独立的，则对于\(x_n\)有下面简化的后验（其只取决于自己的样本）： \[x_n\sim p(x_n|\{x_n^i|i\in I_n\})\]

本文的情况和上述的第二种情况比较类似，即我们没有意愿去求解所有样本的隐变量所共同遵循的分布的性质，即下面的\(\bar{z}\)的性质： \[x^{(i)}_n\sim p(x_n^{(i)}|z^{(i)}_n)\quad z_n\sim p(z_n|\bar{z}) \quad \bar{z}\sim p(\bar{z})\] 得到后验 \[\bar{z}\sim p(\bar{z}|\{x_n^{(i)}\})\] 我们仅仅关注于\(p(z^{(i)})\)，所有是下面的模型： \[x^{(i)}_n\sim p(x_n^{(i)}|z^{(i)}_n)\quad z_n\sim p(z_n)\] 得到后验 \[z_n\sim p(z_n|\{x_n^{(i)}\})\] 这里\(z_n\)只取决于其自己的样本。

另外，在本文中，一个\(z_n\)只能对应一个样本\(x_n\)，所以上面的大括号也不用加：

\[z_n\sim p(z_n|x_n)\]

这里的符号、格式、上下标和文章中的不符，后面会改成和文章符合的格式 \[z^{(i)} \sim p(z^{(i)}|x^{(i)})\]

从编码理论上来看，\(q_{\phi}(z|x)\)可以看做是一个encoder，而\(p_{\theta}(x|z)\)可以看做是一个decoder。

2. 变分下界

结合上面提到的关于单个样本的隐变量的讨论，以及式5，我们可以得到下面的公式（整体的边际似然可以是单个样本的似然的乘积，所以这里只针对单个样本的边际似然进行讨论）：

\[\log p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}\right)=D_{K L}\left(q_{\boldsymbol{\phi}}\left(\mathbf{z} | \mathbf{x}^{(i)}\right) \| p_{\boldsymbol{\theta}}\left(\mathbf{z} | \mathbf{x}^{(i)}\right)\right)+\mathcal{L}\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{x}^{(i)}\right) \tag{7}\]

其中ELBO可以写成：

\[\log p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}\right) \geq \mathcal{L}\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{x}^{(i)}\right)=\mathbb{E}_{q_{\phi}(\mathbf{z} | \mathbf{x})}\left[-\log q_{\boldsymbol{\phi}}(\mathbf{z} | \mathbf{x})+\log p_{\boldsymbol{\theta}}(\mathbf{x}, \mathbf{z})\right] \tag{8}\]

或者另一个形式：

\[\mathcal{L}\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{x}^{(i)}\right)=-D_{K L}\left(q_{\boldsymbol{\phi}}\left(\mathbf{z} | \mathbf{x}^{(i)}\right) \| p_{\boldsymbol{\theta}}(\mathbf{z})\right)+\mathbb{E}_{q_{\boldsymbol{\phi}}\left(\mathbf{z} | \mathbf{x}^{(i)}\right)}\left[\log p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)} | \mathbf{z}\right)\right] \tag{9}\]

现在我们试着针对这个ELBO进行Monte Carlo梯度估计，但使用Monte Carlo梯度估计需要从带有参数\(\phi\)的分布中采样，这会使得结果对于\(\phi\)不可导。

当然，还有另外的办法，也可以使用RL中的方法（如pyro的tutorial中给出了一个推导）：

\[ \begin{aligned} \nabla_{\phi} \mathbb{E}_{q_{\phi}(\mathbf{z})}\left[f_{\phi}(\mathbf{z})\right]&=\nabla_{\phi} \int d \mathbf{z} q_{\phi}(\mathbf{z}) f_{\phi}(\mathbf{z})\\ &=\int d \mathbf{z}\left\{\left(\nabla_{\phi} q_{\phi}(\mathbf{z})\right) f_{\phi}(\mathbf{z})+q_{\phi}(\mathbf{z})\left(\nabla_{\phi} f_{\phi}(\mathbf{z})\right)\right\} \\ &=\mathbb{E}_{q_{\phi}(\mathbf{z})}\left[\left(\nabla_{\phi} \log q_{\phi}(\mathbf{z})\right) f_{\phi}(\mathbf{z})+\nabla_{\phi} f_{\phi}(\mathbf{z})\right] \end{aligned} \]

其中

\[\nabla_{\phi} q_{\phi}(\mathbf{z})=q_{\phi}(\mathbf{z}) \nabla_{\phi} \log q_{\phi}(\mathbf{z})\]

但这个方法得到的估计方差太大，很难使用，要不然就得采大量的样本来降低方差。针对此问题，本研究提出了一个更加有针对性的策略--即重参数化技巧。

3. SGVB估计器和AEVB算法

3.1 SGVB来最小化ELBO

这里会产生两个版本的SGVB estimator：

1. 第一个版本，使用重参数化技巧对公式9进行处理，得到：

   利用后面会介绍的reparameterization trick，可以将\(\phi\)从期望里面移出来：

   \[\widetilde{\mathbf{z}}=g_{\phi}(\boldsymbol{\epsilon}, \mathbf{x}) \quad with \quad \boldsymbol{\epsilon} \sim p(\boldsymbol{\epsilon})\]

   然后就可以使用Monte Carlo方法估计期望：

   \[\mathbb{E}_{q_{\phi}\left(\mathbf{z} | \mathbf{x}^{(i)}\right)}[f(\mathbf{z})]=\mathbb{E}_{p(\boldsymbol{\epsilon})}\left[f\left(g_{\boldsymbol{\phi}}\left(\boldsymbol{\epsilon}, \mathbf{x}^{(i)}\right)\right)\right] \simeq \frac{1}{L} \sum_{l=1}^{L} f\left(g_{\boldsymbol{\phi}}\left(\boldsymbol{\epsilon}^{(l)}, \mathbf{x}^{(i)}\right)\right) \quad where \quad \boldsymbol{\epsilon}^{(l)} \sim p(\boldsymbol{\epsilon})\]

   只需要使用这个技术，即得到了我们的SGVB estimator：

   \[\begin{aligned} \widetilde{\mathcal{L}}^{A}\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{x}^{(i)}\right) &=\frac{1}{L} \sum_{l=1}^{L} \log p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}, \mathbf{z}^{(i, l)}\right)-\log q_{\boldsymbol{\phi}}\left(\mathbf{z}^{(i, l)} | \mathbf{x}^{(i)}\right) \\ \text { where } \quad \mathbf{z}^{(i, l)} &=g_{\boldsymbol{\phi}}\left(\boldsymbol{\epsilon}^{(i, l)}, \mathbf{x}^{(i)}\right) \quad \text { and } \quad \boldsymbol{\epsilon}^{(l)} \sim p(\boldsymbol{\epsilon}) \end{aligned} \tag{10}\]

2. 第二个版本，对第一个版本的进一步细化。如果我们能够将式9中的KL散度显式的写出来，则我们只需要对后面那一项使用Monte Carlo采样估计即可：

   \[\widetilde{\mathcal{L}}^{B}\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{x}^{(i)}\right)=-D_{K L}\left(q_{\boldsymbol{\phi}}\left(\mathbf{z} | \mathbf{x}^{(i)}\right) \| p_{\boldsymbol{\theta}}(\mathbf{z})\right)+\frac{1}{L} \sum_{l=1}^{L}\left(\log p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)} | \mathbf{z}^{(i, l)}\right)\right) \\ \text{where} \quad \mathbf{z}^{(i, l)}=g_{\boldsymbol{\phi}}\left(\boldsymbol{\epsilon}^{(i, l)}, \mathbf{x}^{(i)}\right) \quad \text{and} \quad \boldsymbol{\epsilon}^{(l)} \sim p(\boldsymbol{\epsilon}) \tag {11}\]

3.2 AEVB算法极大化边际似然估计模型参数

我们能够估计ELBO之后，就可以做极大边际似然了：

\[\mathcal{L}(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{X}) \simeq \widetilde{\mathcal{L}}^{M}\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{X}^{M}\right)=\frac{N}{M} \sum_{i=1}^{M} \widetilde{\mathcal{L}}\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{x}^{(i)}\right) \tag{12}\]

其中\(M\)是每个minibatch使用的样本的数量，\(N\)表示对于每个样本进行Monte Carlo计算期望使用的采样数量，在实验中发现，\(N=1\)就有不错的效果。整个过程可以通过SGD系列算法进行。

这里，我的理解：正常的步骤，
第一步更新\(\phi\)最大化ELBO，则此时使得后验的估计是准确的。在后验估计准确的情况下，ELBO等于边际似然。
第二步，更新\(\theta\)最大化ELBO，此时等价于最大化边际似然。
以上两个步骤重复进行，类似EM。
但我们又可以知道，如果交替训练可以找到最优点，则不交替训练也一定能找到最优点，所以我们直接一起训练反而能够找到更好的结果。

在AEs的角度来看式6，我们能够看到其每一项的意义。
第一项是一个regularization，用来尽量保证后验和先验相同；
第二项是一个negative reconstruction loss。
即整个ELBO的含义在于，在保证后验估计和先验尽量相似的情况下，最小化重建误差；或者是在尽量缩小重建误差的情况下，最小化后验估计和先验的差距就能得到准确的后验估计。

4. 重参数化技巧

其需要解决的问题：我们计算梯度的过程中需要进行采样，采样的分布上有我们需要估计的参数，则梯度流无法通过“采样”这个过程，所以无法进行估计。

解决方法：把需要采样的那个分布\(z\sim q_{\phi}(z|x)\)表示成\(z=g_{\phi}(\epsilon, x)\text{,}\quad \epsilon\sim q(\epsilon)\)，这样参数就被移出了采样过程。

示例：现在我们需要采样进行期望估计的分布为\(z \sim p(z | x)=\mathcal{N}\left(\mu, \sigma^{2}\right)\)，则我们可以表示为\(z=\mu+\sigma\epsilon\)，其中\(\epsilon\sim\mathcal{N}(0,1)\)，这时我们发现实际上z还是服从原来的分布的，则我们会有下面的期望估计的变化：

\[\mathbb{E}_{\mathcal{N}\left(z ; \mu, \sigma^{2}\right)}[f(z)]=\mathbb{E}_{\mathcal{N}(\epsilon ; 0,1)}[f(\mu+\sigma \epsilon)] \simeq \frac{1}{L} \sum_{l=1}^{L} f\left(\mu+\sigma \epsilon^{(l)}\right) \\ \text { where } \epsilon^{(l)} \sim \mathcal{N}(0,1)\]

要能够使用重参数化技巧，意味着\(q_{\phi}(z|x)\)必须满足一定的条件：

1. 可以知道\(q_{\phi}(z|x)\)的inverse CDF。我们假设这个inverse CDF为\(g_{\phi}(\epsilon, x)\)，则取\(\epsilon\sim\mathcal{U}(0,I)\)即可。比如：Exponential, Cauchy, Logistic, Rayleigh, Pareto, Weibull, Reciprocal, Gompertz, Gumbel and Erlang distributions
2. 像gaussian一样，其参数是location scale的，即表示的是平移、缩放。则可以表示\(g(.)=location+scale\cdot\epsilon\)，其中\(\epsilon\)服从那个在location=0、scale=1的那个分布。比如：Laplace, Elliptical, Student’s t, Logistic, Uniform, Triangular and Gaussian distributions
3. 可以分解为不同的容易处理的组分的。比如：Log-Normal (exponentiation of normally distributed variable), Gamma (a sum over exponentially distributed variables), Dirichlet (weighted sum of Gamma variates), Beta, Chi-Squared, and F distributions

5. 变分自编码器

以上相对于为研究人员提供了一个框架。其中还没有假设\(p(z)\)、\(p(z|x)\)和\(p(z|x)\)的形式。

以下便是最常用的一种：

1. 认为latent variables的prior是独立的标准正态分布。
   • 了解贝叶斯统计的可以知道，如果样本量够大，样本的影响会基本彻底淹没先验的影响，这时候先验取什么对后验的影响是非常小的；
   • 这个有点像岭回归，相对于只是起一个对隐变量的微小约束。如果没有这个约束，隐变量可以取任意的值，这显然不合理，而且估计的方差也会很大。从岭回归的角度，这相当于限制隐变量估计的方差。
   • 对于一个没有任何其他知识的隐变量的估计，我们预先的认为其不会很大（这就是标准正态先验的含义）是合理的。
2. \(p_{\theta}(x|z)\)是经过NN输出参数化的独立Gaussian或Bernoulli。
3. 认为\(p_{\theta}(z|x)\)是经过NN输出参数化的独立Gaussian。
   • 2和3的含义即认为确定的\(x\)或\(z\)对应的\(z\sim p(z|x)\)或\(x\sim p(x|z)\)依然是个分布，但是是一个在预测值周围震荡的gaussian或Bernoulli，这没有什么限制，毕竟是将其非线性变换后的（如果NN换成线性，不就是OLS和Logistic嘛）。

对于\(q_{\phi}(x|z)\)的选择就随意多了，我们让它和\(p_{\theta}(x|z)\)有相同的形式。所以在上面的2假设成立的情况下，则我们会得到最优解。如果上面的2假设不成立，那么我们也不会有太大的损失（比较前面有NN，使得我们能够拟合成一个Gaussian的机会大大增加了）(不好理解就类比线性模型)。

经过一阵推导，得到下面的loss公式：

\[\mathcal{L}\left(\boldsymbol{\theta}, \boldsymbol{\phi} ; \mathbf{x}^{(i)}\right) \simeq \frac{1}{2} \sum_{j=1}^{J}\left(1+\log \left(\left(\sigma_{j}^{(i)}\right)^{2}\right)-\left(\mu_{j}^{(i)}\right)^{2}-\left(\sigma_{j}^{(i)}\right)^{2}\right)+\frac{1}{L} \sum_{l=1}^{L} \log p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)} | \mathbf{z}^{(i, l)}\right)\tag{13}\]

\[\text { where } \mathbf{z}^{(i, l)}=\boldsymbol{\mu}^{(i)}+\boldsymbol{\sigma}^{(i)} \odot \boldsymbol{\epsilon}^{(l)} \quad \text { and } \quad \boldsymbol{\epsilon}^{(l)} \sim \mathcal{N}(0, \mathbf{I})\]

loss的第二项根据数据的形式（continuous or binary）选择Gaussian或Bernoulli的形式。

关于KL散度项的推导和后面的重构项在不同的情况下怎么计算，将在supplementary部分解释。

Related work

1. wake-sleep算法【HDFN95】是目前为止已知的和本研究一样general的continuous latent variables建模方法。其缺点是需要2-steps的optimization（有两个目标函数）。优点是可以应用于discrete latent variables。其计算复杂度和AEVB相当。
2. 在Stochastic variational inference【HBWP13】的领域，一些研究通过限制一些技巧可以控制gradient estimator的方差【BJP12】、【RGB13】，而【SK13】使用了类似的重参数化技巧。
3. 之前已经有相关研究【Row98】，探索PCA和ML的结合，相对于是使用linear AEs。
4. AEs方面的最新研究【VLL+10】，试图去最小化\(X\)和\(Z\)之间的MI，但这个regularization不如本文的方法自然；【BTL13】使用Markov Chain的样本来训练noisy的AEs。
5. 【GMW13】、【RMW14】和本文类似的结果，但各研究之间是独立进行的。

Experiments

在MNIST和Frey Face数据集上进行了实验，并和其他算法进行了比较。

在decoder的输出层是sigmoid，使之归一化到0-1。参数采样自\(\mathcal{N}(0, 0.01)\)，使用Adagrad进行训练。minibatch size是100。对于MNIST，encoder hidden是500；对于Frey Face则是200。

1. 首先是lower bound的比较，AEVB能够得到更大的lower bound

   
   

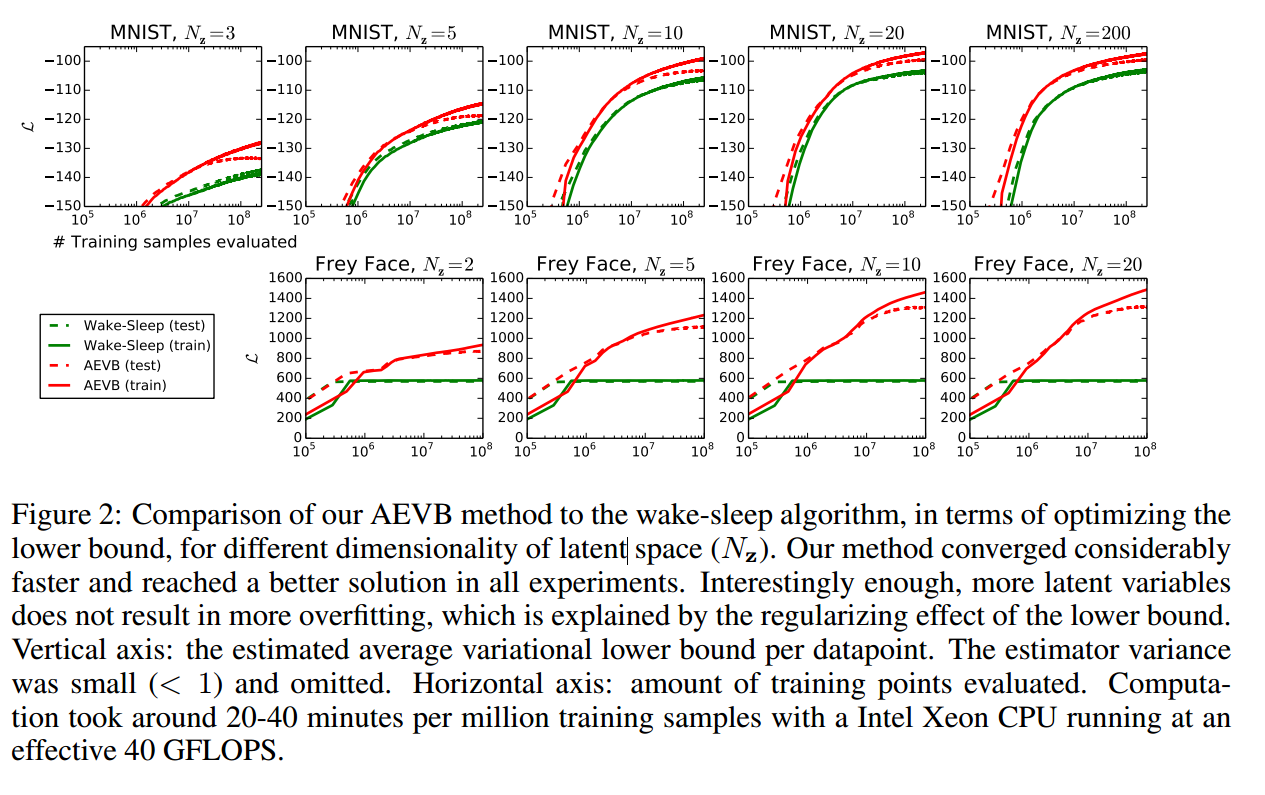
2. 和MCMC EM方法、wake-sleep方法比较了一下边际似然，发现AEVB还是好的。

   
   

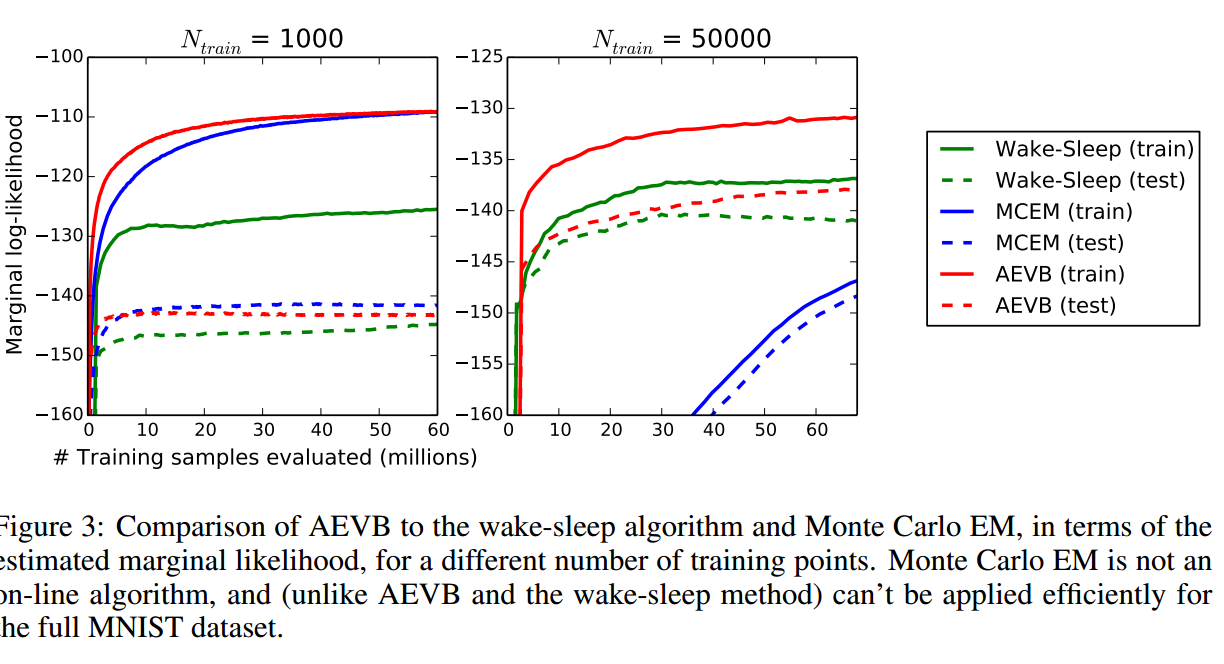
3. 高维数据的可视化：

   
   

   
   

Conclusion

未来：

• CNNs；
• 时间序列数据；
• 应用到global paramters；
• 应用到supervised models。

Supplementary

1. 损失函数中KL散度项的求解

这里使用前面VAE的假设，即\(p(\mathbf{z})\)独立标准正态，\(q_{\phi}(\mathbf{z}|\mathbf{x}^{(i)})\)是独立正态：

\[ \begin{aligned} p(\mathbf{z})&=\mathcal{N}(0, I) \\ &=\prod_{i=1}^{d}{\frac{1}{\sqrt{2\pi}}\exp{(-\frac{z_i^2}{2})}} \end{aligned} \]

\[ \begin{aligned} q_{\phi}(\mathbf{z}|\mathbf{x}^{(i)}) &=\mathcal{N}(\mathbf{\mu},\mathbf{\sigma}^2) \\ &=\prod_{i=1}^d{\frac{1}{\sqrt{2\pi}\sigma_i}\exp{(-\frac{(z_i-\mu_i)^2}{2\sigma_i^2})}} \end{aligned} \] 其中\(\mu_i=\mu_{\phi}(x^{(i)})\)，\(\sigma_i=\sigma_{\phi}(x^{(i)})\)，将\(x^{(i)}\)输入NN计算得到的。

我们将KL散度拆成两项分别计算，得到：

\[\begin{aligned} -D_{K L}\left(\left(q_{\phi}(\mathbf{z}) \| p_{\boldsymbol{\theta}}(\mathbf{z})\right)\right.&=\int q_{\boldsymbol{\theta}}(\mathbf{z})\left(\log p_{\boldsymbol{\theta}}(\mathbf{z})-\log q_{\boldsymbol{\theta}}(\mathbf{z})\right) d \mathbf{z} \\ &=\frac{1}{2} \sum_{j=1}^{J}\left(1+\log \left(\left(\sigma_{j}\right)^{2}\right)-\left(\mu_{j}\right)^{2}-\left(\sigma_{j}\right)^{2}\right) \end{aligned}\]

其中

\[\begin{aligned} \int q_{\boldsymbol{\theta}}(\mathbf{z}) \log p(\mathbf{z}) d \mathbf{z} &=\int \mathcal{N}\left(\mathbf{z} ; \boldsymbol{\mu}, \boldsymbol{\sigma}^{2}\right) \log \mathcal{N}(\mathbf{z} ; \mathbf{0}, \mathbf{I}) d \mathbf{z} \\ &=-\frac{J}{2} \log (2 \pi)-\frac{1}{2} \sum_{j=1}^{J}\left(\mu_{j}^{2}+\sigma_{j}^{2}\right) \end{aligned}\]

\[\begin{aligned} \int q_{\boldsymbol{\theta}}(\mathbf{z}) \log q_{\boldsymbol{\theta}}(\mathbf{z}) d \mathbf{z} &=\int \mathcal{N}\left(\mathbf{z} ; \boldsymbol{\mu}, \boldsymbol{\sigma}^{2}\right) \log \mathcal{N}\left(\mathbf{z} ; \boldsymbol{\mu}, \boldsymbol{\sigma}^{2}\right) d \mathbf{z} \\ &=-\frac{J}{2} \log (2 \pi)-\frac{1}{2} \sum_{j=1}^{J}\left(1+\log \sigma_{j}^{2}\right) \end{aligned}\]

2. 指定样本的边际似然的计算

1. 使用MCMC方法对\(\mathbf{z}\)进行采样（现在我们知道先验--标准正态、似然--我们拟合的\(p_{\theta}(x|z)\)，我们自然可以使用MCMC进行采样）。
2. 将这些使用这些样本拟合一个密度估计器\(q(\mathbf{z})\)（实际上拟合的不是整体的后验吗？）。
3. 从确定的某个样本\(x^{(i)}\)的后验分布中进行采样，利用上一步得到的密度估计器，计算下面的估计：

\[p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}\right) \simeq\left(\frac{1}{L} \sum_{l=1}^{L} \frac{q\left(\mathbf{z}^{(l)}\right)}{p_{\boldsymbol{\theta}}(\mathbf{z}) p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)} | \mathbf{z}^{(l)}\right)}\right)^{-1} \text {where } \mathbf{z}^{(l)} \sim p_{\boldsymbol{\theta}}\left(\mathbf{z} | \mathbf{x}^{(i)}\right)\]

这个估计的推导如下所示：

\[\begin{aligned} \frac{1}{p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}\right)} &=\frac{\int q(\mathbf{z}) d \mathbf{z}}{p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}\right)}=\frac{\int q(\mathbf{z}) \frac{p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}, \mathbf{z}\right)}{p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}, \mathbf{z}\right)} d \mathbf{z}}{p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}\right)} \\ &=\int \frac{p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}, \mathbf{z}\right)}{p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}\right)} \frac{q(\mathbf{z})}{p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}, \mathbf{z}\right)} d \mathbf{z} \\ &=\int p_{\boldsymbol{\theta}}\left(\mathbf{z} | \mathbf{x}^{(i)}\right) \frac{q(\mathbf{z})}{p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)}, \mathbf{z}\right)} d \mathbf{z} \\ & \simeq \frac{1}{L} \sum_{l=1}^{L} \frac{q\left(\mathbf{z}^{(l)}\right)}{p_{\boldsymbol{\theta}}(\mathbf{z}) p_{\boldsymbol{\theta}}\left(\mathbf{x}^{(i)} | \mathbf{z}^{(l)}\right)} \quad \text { where } \quad \mathbf{z}^{(l)} \sim p_{\boldsymbol{\theta}}\left(\mathbf{z} | \mathbf{x}^{(i)}\right) \end{aligned}\]

3. full VB

这里将神经网络的参数也视为一个随机变量，则使用变分推断时，推断的不止是隐变量，还有参数的分布。类似贝叶斯神经网络的思想。这里也是文中关于“global parameters”的部分。

---

Questions

1. 我按照论文中的介绍，实现了一下，发现即使是在MNIST上也出现了一些问题:

   • loss中的kl项会降至0，而reconstruction项基本不怎么降，或者降的幅度不大。
   • 使用训练好的模型进行采样，采不出样本或者采到的都是相同的模糊样本。

   我查阅了一些资料，怀疑是“KL vanishing”的问题：

   KL vanishing指的是我们的模型陷入到了一个特殊的局部最小值中，这个局部最小值具有以下特点：

   • encoder并不会将X的信息编码到Z中，只是让得到的Z和P(Z)的KL散度变为0
   • 因为Z中没有X的信息，所以\(p(X|Z)=p(X)\)（Z和X独立），如果decoder足够强大，其会自己来生成\(p(X)\)的分布，这时候decoder自己变成了一个概率模型

   造成这个的原因一般有两个：

   • 最小化KL散度比最小化重构误差容易（原始的VAE确实容易这样，因为我们毕竟只是在最小化和Gaussian的差异，Gaussian还是简单的），我们很容易就先最小化了KL。
   • decoder太强，这在一些做NLP的工作中经常出现，因为做NLP需要将decoder做的比较强。

   以后可能会单独就这个问题进行研究，现在先提供一个较为简单的解决方案：

   • 在KL loss项前乘以一个较小的权重，降低其重要性（PyTorch-VAE中是这样实现的，我是直接乘了一个0.001效果就不错），或者使这个权重在训练的过程中从0逐步增大到1（KL cost annealing），保证encoder可以学习到X的信息

   当然还有其他的方法：比如不让KL降的太小、使用flow来代替单纯的Gaussian、使用cycleGAN的思想添加一个从X_rec返回到Z的路径并最小化两个Z间的差距（保证X中含有Z的信息）、各种降低decoder能力的方法（这个可能并不是我的model出现问题的原因）。