MADE: Masked Autoencoder for Distribution Estimation
- 杂志: None
- IF: None
- 分区: None
- source code
Introduction
一个general的问题是如何从一组数据中得到其概率密度估计,一个好的概率密度估计器可以用于许多下游任务。“维数灾难”是该任务的主要困难之一。
最近,在深度学习领域,该问题得到了长足的进步,显示出了巨大的潜力。
本研究专注于autoregressive model,之前对此的研究一直没有解决computational cost的问题,本研究通过一种简单的方法来加快估计的速度——使用masking的方法,将一个autoencoder改造成一个autogregressive model,称为MADE。
早期的单层版本是【Bengio & Bengio (2000)】,本研究中将试着将其加深,并在一个binary datasets with hundreds of dimensions上进行测试。
Related Works
- NADE【Larochelle & Murray, 2011】
- NADE的深度扩展【Uria et al., 2014】,表现不错,但时间花费较多
- DARN【Gregor et al., 2014】
另外,可以将MADE看做是结构化的dropout【Srivastava et al., 2014,Wan et al., 2013】。
以下是几种方法的时间复杂度:

Methods
本研究关注于每个变量是binary code的数据的概率密度估计。
Autoencoders
略
Autoregression
我们首先将整个概率密度进行分解:
\[p(X)=\prod_{d=1}^Dp(x_d|X_{\lt d})\]
其中\(X_{\lt d}=(x_1, \dots, d_{d-1})^T\)。则negative log-likelihood是:
\[ \begin{aligned} -\log p(X)&=\sum_{d=1}^D -\log p(x_d|X_{\lt d}) \\ &=\sum_{d=1}^D [-x_d\log p(x_d=1|X_{\lt d})]\cdot [-(1-x_d)\log p(x_d=0|X_{\lt d})] \\ &=l(X) \end{aligned} \]
我们可以看到,只需要我们让AEs的输出中的每个神经元,其只依赖于其前面的神经元,则AEs自然形成一个Autoregressive model。这称为autoregressive property。
Masked Autoencoders
实现的一个方式是给fc中的weight乘上一个masked matrix,使得我们不希望存在的依赖关系为0。
考虑一个只有bottle neck layer(维度是\(K\))的AE:
\[ h(X) = g(B+X(W\odot M^W)) \\ \hat{X} = \sigma(C+h(X)(V\odot M^V)) \] 其中\(M^W\)和\(M^V\)表示masked matrices,维度分别是\(D\times K\)和\(K\times D\)。
设\(m(k)\)表示第\(k\)个瓶颈层神经元连接的输入的个数(其取值是\(\{1,\cdots,D-1\}\)),则两个masked matrices的设置为:
\[ M^W_{k,d} = \mathbf{1}_{m(k)\ge d} = \begin{cases} 1 \quad if\ m(k)\ge d \\ 0 \quad otherwise \end{cases} \]
以下是一个\(4\times 5\)的例子,我们假设瓶颈层的神经元分别连接1、2、3、4个神经元:
\[ M^W = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 1 & 0 \end{pmatrix} \] 这时候,注意,最后一个个输入神经元\(x_D\)是不会连接的。这是合理的,因为分解后的分量中并不存在以最后一个分量\(x_D\)为条件的条件概率。
\[ M^V_{d,k} = \mathbf{1}_{m(k)\lt d} = \begin{cases} 1 \quad if\ m(k)\lt d \\ 0 \quad otherwise \end{cases} \]
继续上面的例子:
\[ M^V = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 1 \end{pmatrix} \] 这时候,第一个输出神经元\(\hat{x}_1\)不会有连接。这也是合理的,因为分解后的分量中不会有\(p(x_1|...)\)的分量,其是\(p(x_1)\)是自己先验生成的。
进一步我们可以看到,有\(K\ge D-1\),不然将没有足够的链接构筑所有的条件分量。\(K\)大一点则没有关系,只是会出现一些重叠作用的神经元而已。
以上的依赖关系从矩阵上看不太直观,自己在纸上画一些连接关系就一目了然了。
另外,我们没有必要像上面的例子一样来设置\(m(k)\)(\(m(k)=k\),实际上本研究后续的实验中是随机的分配这个\(m(k)\)的,只要保证其包含所有的\(\{1,\cdots,D-1\}\)。
我们将两个矩阵相乘,得到:
\[ M^{V,W}_{d',d}=\sum_{k=1}^K{M^V_{d',k}M^W_{k,d}}= \sum_{k=1}^K{\mathbf{1}_{d\le m(k)}\mathbf{1}_{m(k)\lt d'}} \]
这个元素表示的是\(d'\)是否对\(d\)有依赖。如果\(d'\gt d\),我们发现是存在\(m(k)\)满足上面的条件的,所以上面是1,不然则上面的值为0。如果\(d'\le d\),则满足上面条件的\(m(k)\)不会存在,所以这样的依赖关系也不会存在。满足了autoregressive property。
以上的公式也佐证了\(m(k)\)必须遍历所有的\(\{1,\cdots,D-1\}\),不然,比如说\(\forall k,m(k)\ne 3\),则当\(d'=4,d=3\)时,以上的值为\(0\),也就是说\(x_4\)的生成将无法依赖于\(x_3\),这对于自回归模型当然是错的。
在【Bengio & Bengio, 2000】中进一步进行了改进:
\[\hat{X}=\sigma(C+h(X)(V\odot M^V)+X(A\odot M^A))\]
即加了一个skip connect,这将有助于训练。
Deep MADE
类似上面的想法,我们为每个神经元都分配一个最大连接数,则可以类似的在更深的网络上构建自回归模型。
假设第\(l\)层的weight matrix为\(W^l\),这一层的神经元个数为\(K^l\),则\(W^l\)的维度是\(K^{l-1}\times K^l\),\(K^0\)是输入维度。第\(l\)层的第\(k\)个神经元接受的连接数为\(m^l(k)\)。我们进行下面的分配:
\[ M^{W^l}_{k',k} = \mathbf{1}_{m^l(k')\ge m^{l-1}(k)}= \begin{cases} 1 \quad if\ m^l(k')\ge m^{l-1}(k) \\ 0 \quad otherwise \end{cases} \]
在最后一层,则使用输入维度\(D\)作为输出维度:
\[ M^{V}_{d,k} = \mathbf{1}_{d\gt m^L(k)}= \begin{cases} 1 \quad if\ d\gt m^L(k) \\ 0 \quad otherwise \end{cases} \]
将以上这些矩阵连乘,得到输入和输出的连接模式(\(L\)个隐层,还有一个输出层):
\[ \begin{aligned} M^{V,W^L,\dots,W^1}_{d',d} &=\sum_{k^1,k^2,\dots,k^L} {M^{W^1}_{d,k^1}M^{W^2}_{k^1,k^2}\cdots M^{W_L}_{k^{L-1},k^l}M^V_{k^L,d}} \\ &=\sum_{k^1,k^2,\dots,k^L} {\mathbf{1}_{d\le m^1(k^1)}\mathbf{1}_{m^1(k^1)\le m^2(k^2)}\cdots\mathbf{1}_{m^{L-1}(k^{L-1})\le m^L(k^L)}\mathbf{1}_{m^L(k^{L})\lt d'}} \tag{1} \end{aligned} \]
有上面的式子可以知道,为了避免漏掉可能的依赖关系,则\(m^l(k)\ge \min_{k'}{m^{l-1}(k')}\)。只有这样,才能保证中间的所有不等式在\(d'\gt d\)时有成立的可能,从而算出来值为1。
同样的我们可以知道,其中的\(m^l(k^l)\)的取值必须使得\(d'\gt d\)时有成立的可能。因为多层的缘故,我们现在有很多种mask的方式,比如下面的fig1是其中的一种。
类似上一节中对单层网络的讨论,我们知道,只要使得masks满足上面的要求,所以我们希望出现的依赖关系(前面分量对后面分量的依赖,\(d\ge d'\)),是不会出现的。
- 进一步,我们来说明,实际上\(m^l(k^l)\)必须能够将\(\{1,\dots,D-1\}\)的所有值都取遍,不然将遗漏必要的依赖性
autoregressive property 保证了第\(h\)个变量对第\(h-1\)个变量一定有依赖,所以当\(d=h-1\),\(d'=h\)时,上式中必须存在一项是等于1的。也就是说,必须在每一层中存在一个神经元\(\{k^1,\dots,k^L\}\),使得其分配的连接数\(\{m^1(k^1),\dots,m^L(k^L)\}\)使得上面的所有不等式成立。这时我们发现,这个连接数必须是 \[m^1(k^1)=\cdots=m^L(k^L)=h-1\] 显然,\(h\)可以从\(2\)一直取到\(D-1\),所以每一层都必须有神经元拥有这些连接数\(\{1,\dots,D-1\}\)。
这也进一步证明了,每一个隐层的神经元个数必须\(\ge D-1\)。
- 最后我们来证明,只要每一层都保证了取遍\(\{1,\dots,D-1\}\),则所有我们需要的依赖关系都是可以满足的
要让\(d\lt d'\)之间存在依赖关系,需要存在\(\{m^1(k^1),\dots,m^L(k^L)\}\),使得其是一个递增的数列,并且正好在\([d,d')\)之间。显然因为每一层都有\(\{1,\dots,D-1\}\),所以我们这只需要取这个数列是\(\{d,d,\dots,d\}\)即可。
注意到,如果我们设置更多的隐层神经元,则单个依赖关系会有更多的重复路径,则会增强网络的表达能力。
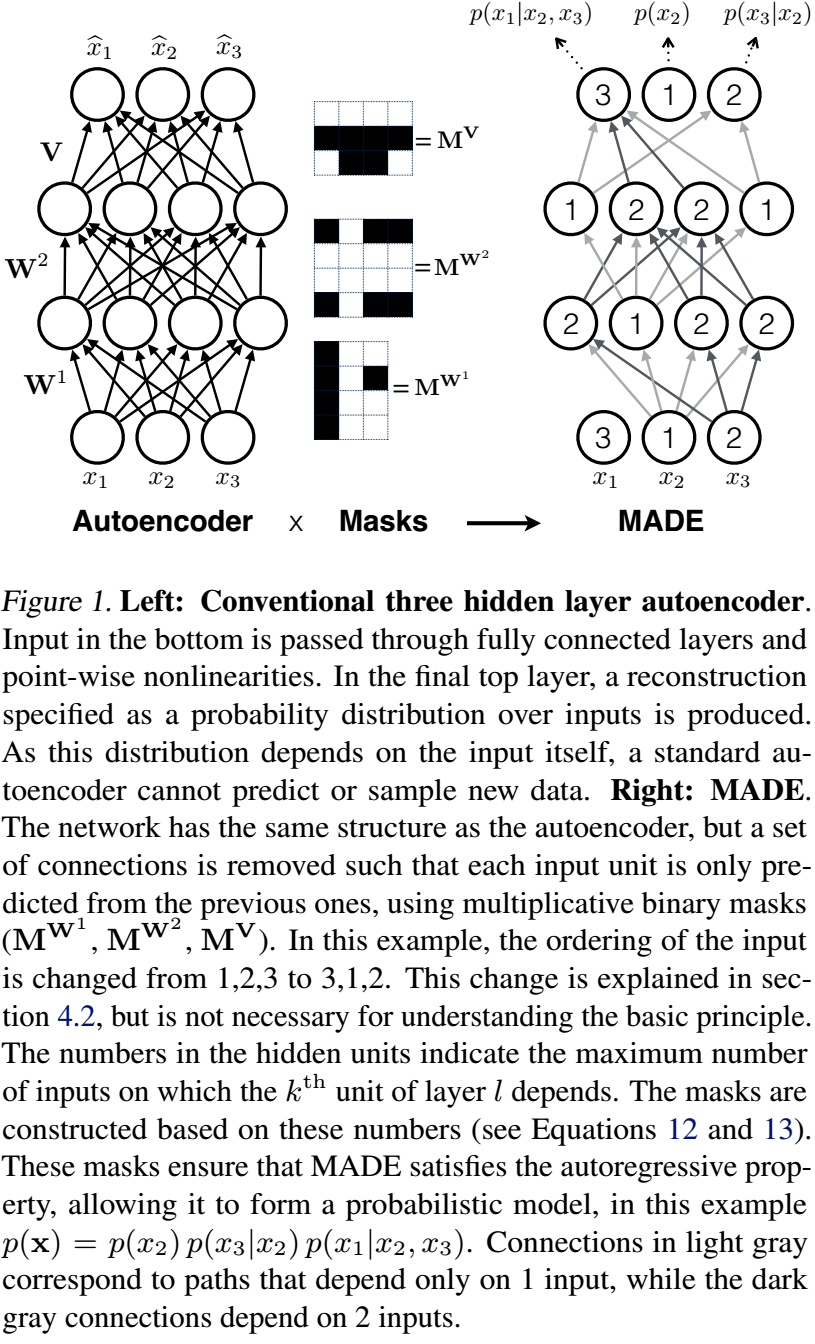
Order-agnostic training
【Uria et al. (2014)】已经证明,在\(X\)向量的全排序上训练autoregressive model是有益的。
而且这也有实际的意义:
- 如果我们当前拥有一个样本的一部分变量,想要将剩下的变量生成,我们可以将这些存在的变量排在前面,然后递归的生成下面的变量,这必须在乱序的model中进行。
- 我们可以快速的构建一个model的ensemble:即以不同的顺序去进行estimate,然后将得到的结果平均。
实现的方法是非常简单的,即在每个minibatch上都使用一种新的ordering进行训练即可(对输入permutate即可)。
Connectivity-agnostic training
类似order-agnostic training,我们也可以在连接模式(masked)上“动手脚”。
即在每个minibatch training之前都重新将每个layer的masked matrices进行重新修改。
但这样训练时有个问题:即输入是0的神经元和被掩盖掉的神经元是无法区分的,这可能会造成训练的困难。【Uria et al. (2014)】提出一个解决方案是在训练的时候另外加上一个被同样掩模处理得到神经元,但这个神经元的输入都是1,这样进行区分,公式为:
\[ \mathbf{h}^{l}(\mathbf{x})=\mathbf{g}\left(\mathbf{b}^{l}+\left(\mathbf{W}^{l} \odot \mathbf{M}^{\mathbf{W}^{l}}\right) \mathbf{h}^{l-1}(\mathbf{x})+\left(\mathbf{U}^{l} \odot \mathbf{M}^{\mathbf{W}^{l}}\right) \mathbf{1}\right) \]
另外,只使用有限种mask可以避免欠拟合。然后在test时对所有的mask都试一遍,然后将输出进行平均。
以下的算法详细介绍了整个算法:

Results
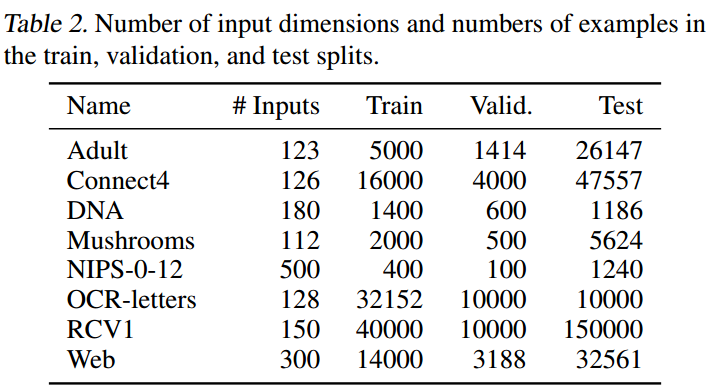
使用的数据集:
- a suite of UCI binary datasets
- the binarized MNIST dataset
评价指标是test上的负对数似然,minibatch size是100,使用earlystop(向前看30步)。
UCI evaluation suite
由7个小型数据集组成,其详细信息如下:
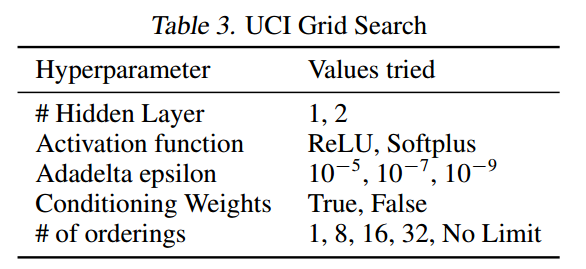
model信息:
- hidden units 500
- decay 0.95
- valid和test时使用的masked的数量是300和1000
- 其他如下表所示
结果如下所示:
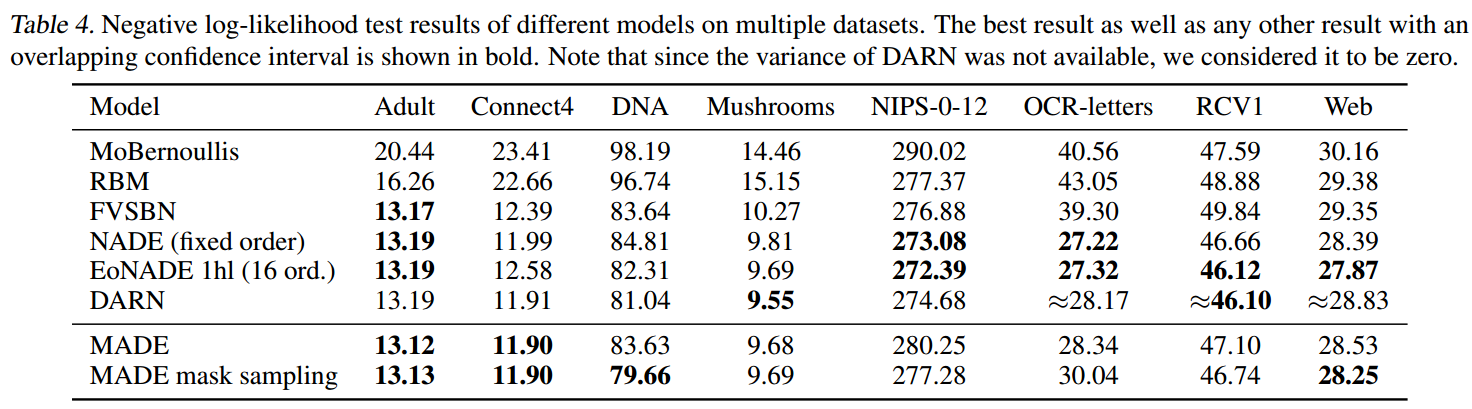
可以看到,MADE相对于其他模型是非常有竞争力的。
MINIST数据集
28x28的pixels,training=50000、valid=10000、test=10000。
model信息:
- hidden units的数量从500试到8000,发现越多越好,所以使用的是8000。
- 其他超参数设置如下
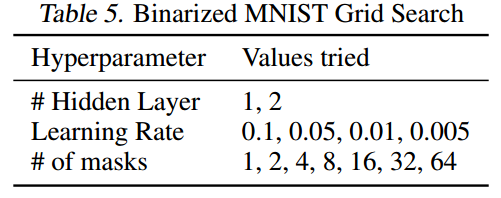
结果如下所示:
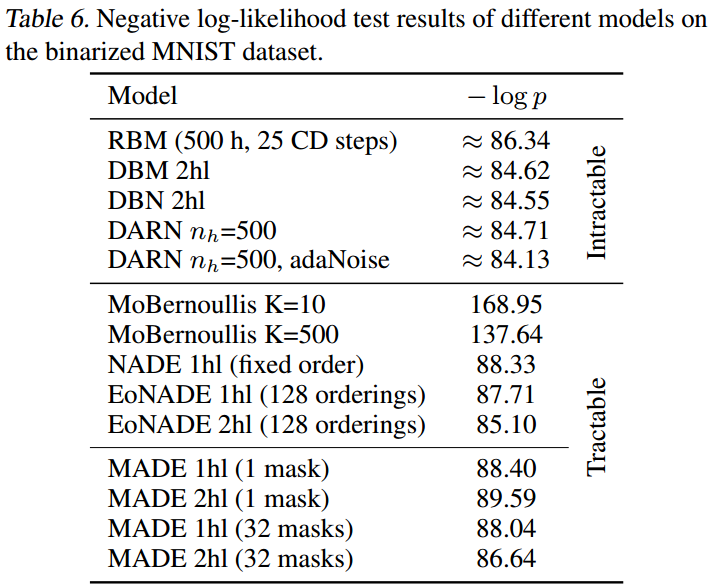
结果显示
MADE是有竞争力的,并且在单层情况下要优于NADE(这是之前单层最好的方法)。
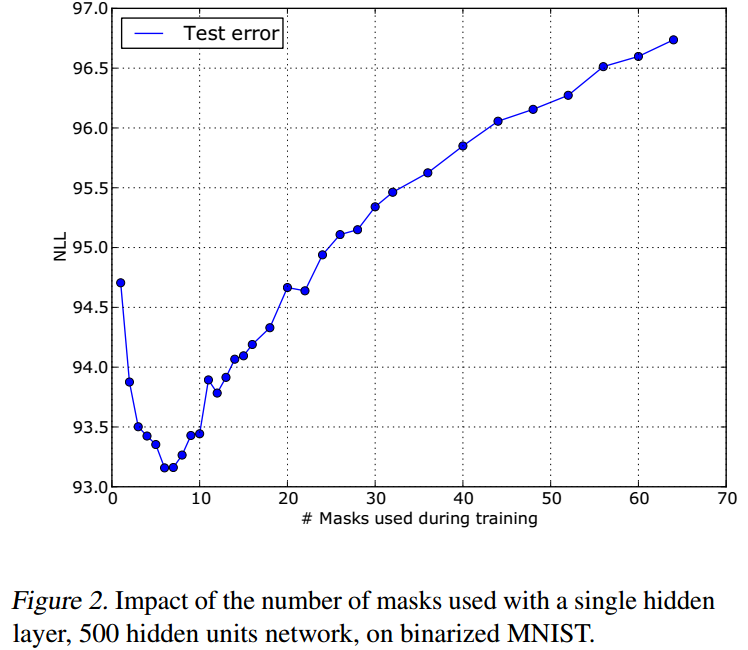
如果使用了太多的masks,将导致明显的欠拟合线性:
从表现最好的model中生成了100个数字,进行了可视化:

Conclusion
MADE可以进行非常高效的概率密度估计,和标准的AEs类似,可以非常方便地利用GPU的算力。
Questions
在上面,我们证明了,如果想要能够让每个条件分量都存在,我们需要让隐层的神经元数量至少为\(D-1\)。但不管在paper中还是github的各种实现中,都没有这个隐层神经元数量的限制?难道是我错了?
在进行实验的时候,我发现order-agnostic的策略并不成功,这是为什么??



