论文精读-对graph的深度学习的深度介绍-2020

Deep Learning Graph Neural Networks
Paper-Review
发布日期:   2020-08-28
更新日期:   2020-12-03
文章字数:   4.8k
阅读时长:   19 分
阅读次数:  

A Gentle Introduction to Deep Learning for Graphs

  • 杂志: None
  • IF: None
  • 分区: None

介绍

  1. graph数据是广泛存在的。

  2. 深度学习在graphs数据上的研究，需要克服几个挑战：

    • 模型需要对不同大小、拓扑结构的graphs可用
    • 节点的信息可能比较稀缺
    • graphs是离散对象，可微性不是很好，而其组合特性又限制了我们使用类似穷举的方法进行求解
    • 有些graphs存在循环

  3. 深度学习在graphs上的研究历史：

    1. 早期就有使用RecNN（递归神经网络）【98,32,9】来对tree structured data进行建模的历史，但其无法处理带有cycles的graphs。
    2. GNN【89】和NN4G【74】可以处理带有cycles的graphs。两者分别为两类方法打下了基础（recurrent-GNN和feedforward-NN4G），特别是后者，是GCN的基础。

  4. 本研究希望能够对DL在graphs上的方法进行一个介绍，涉及的前沿的方法可能比较少，更多地作为一个tutorial，来巩固一些经典算法。

概述

数学符号

graph：\(g=(\mathcal{V}_g, \mathcal{E}_g, \mathcal{X}_g, \mathcal{A}_g)\)

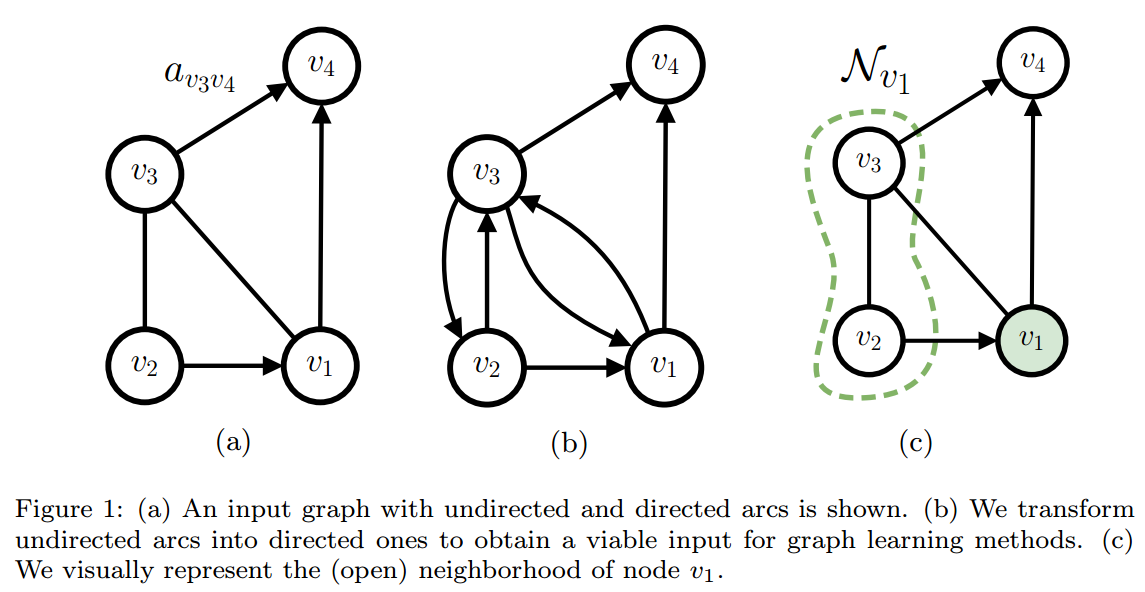
其中节点集合\(\mathcal{V}_g\)，边的集合\(\mathcal{E}_g\)，如果是directed edges，则\(\mathcal{E}_g=\{(u,v)|u,v\in\mathcal{V}_g\}\)，如果是undirected edgs，则认为\((u,v)=(v,u)\)，\(\mathcal{E}_g\)同时拥有两个方向的arcs。有时候可以直接使用邻接矩阵\(\mathbf{A}\in{0,1}^{|\mathcal{V}_g|\times|\mathcal{V}_g|}\)来表示\((\mathcal{V}_g, \mathcal{E}_g)\)。

节点\(v\)上的特征是\(\mathbf{x}_v\in\mathcal{X}_g\)，边\((u,v)\)上的特征是\(\mathbf{a}_{uv}\in\mathcal{A}_g\)。节点、边、整个graph的标签使用\(y_v,y_{uv},y_g\)来表示。

如果graph的节点定义了一个顺序，则称之为是ordered，反之是unordered。如果边的集合和一个自然数的集合存在双射，则称为positional，反之称为non-positional。我们关注的是unordered和non-positional的graph。

节点\(v\)的邻域（neighborhood）定义为\(\mathcal{N}_v=\{u\mathcal{V}_g|(u,v)\in\mathcal{E}_g\}\)。这个也成为了open neighborhood，有时候我们也把\(v\)本身也加入其中，这时称为closed neighborhood。进一步，结合边的特征，我们可以定义特征符合条件的neighborhood\(\mathcal{N}_v^{c_k}=\{u\in\mathcal{N}_v|\mathbf{a}_{uv}=c_k\}\)。

原始文献PDF这里应该是写错了（第6页第3行，应该是v而不是u）

在图论中，neighborhood不是点的集合，而是一个subgraph，是邻接点及其与指定点的边组合成的subgraph。

\(l\)用来表示第\(l\)层或第\(l\)个迭代步骤，\(\mathbf{h}_v^l\)表示节点\(v\)在第\(l\)层或第\(l\)个迭代步骤后得到的特征。

使用\(\Psi\)来表示permutation invariant function。当其输入（一般来说输入是一个集合）的元素数量是可数时，可以大致将其写成下面的形式： \[\Phi(Z)\approx\phi(\sum_{z\in Z}{\psi(z)})\] 其中\(\phi\)和\(\psi\)是任意的函数。


动机

自适应地学习到新的特征进行下游的任务。

概览

不管任务是什么，几乎所有的算法首先都生成节点的表示，这称为graph的isomorphic transduction。然后在此基础上，再根据任务的不同进行后续的操作。

这里，我们DGN来同一描述这些所有的算法，具体来说，是这些算法中从graph到生成节点特征的部分，如下图所示。


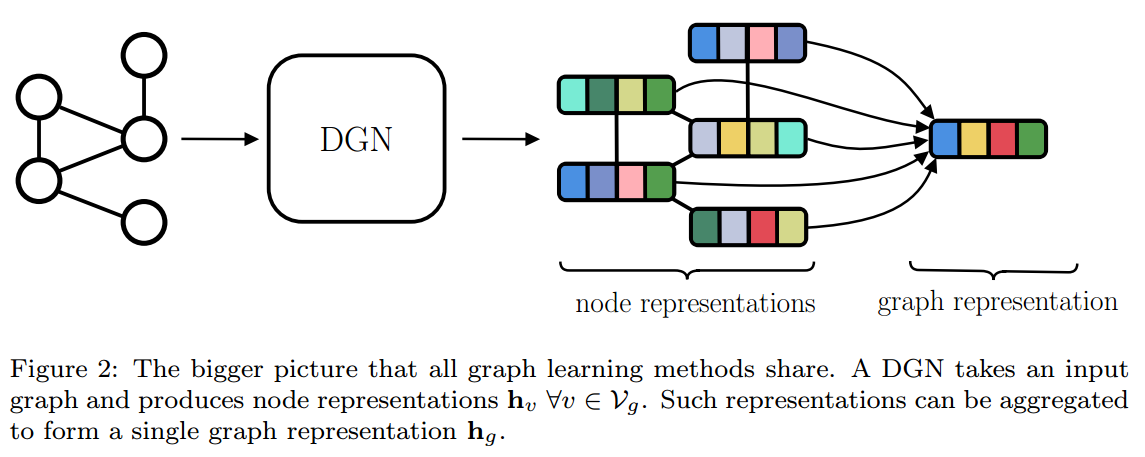
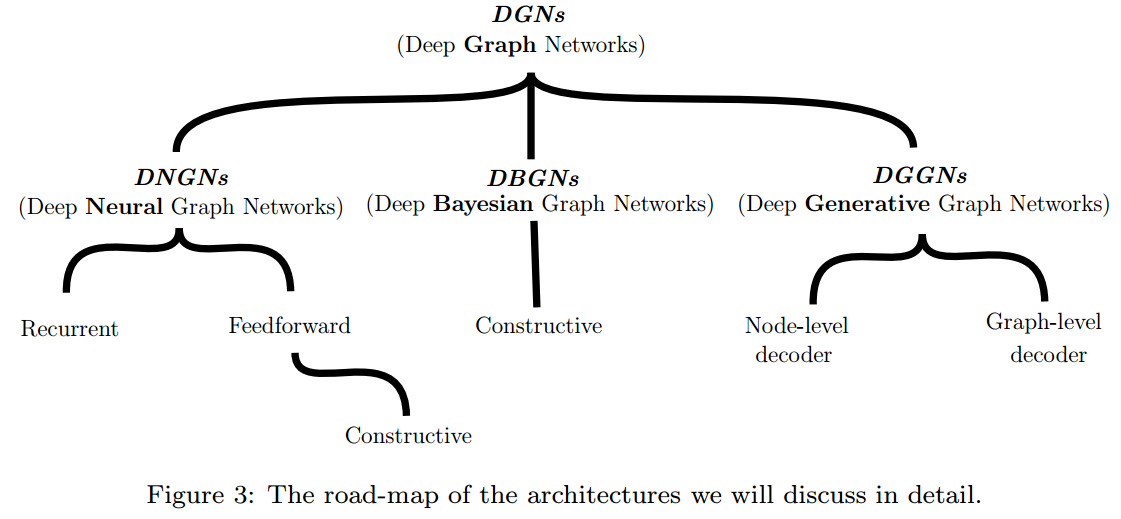
DGN被进一步分为3类：

  • DNGNs（Deep Neural Graph Networks）
  • DBGNs（Deep Bayesian Graph Networks）
  • DGGNs（Deep Generative Graph Networks）


局部关系和信息的迭代处理

对于graph的处理面临以下两个基本问题，而且讨论了其普遍的解决方案（“局部和迭代”方法）。

  • graph的拓扑结构是没有什么限制假设的

    这一般通过在node level局部地而不是在graph level全局地建立模型来完成【98】，即考虑的是节点和其邻节点间的关系。这称为stationary assumption。

    但stationary assumption并没有完全解决问题，因为每个节点所拥有的邻接点的数量是变化的。所以，一般还需要使用permutation invariant function来将邻接点集合进行处理。

  • 可能存在cycle

    解决这个问题的方法是建立迭代机制，即\(\mathbf{h}_v^{l+1}\)是第\(l\)次迭代的邻接点特征计算得到，这样就算是有cycle存在，也可以方便被纳入其中（可以看做自我更新）。另外，迭代机制也可以很方便地集成到深度架构中。

context diffusion的3种机制

context指的是计算节点特征所使用的信息。context diffusion描述的是我们如何将单个节点的信息传递到整个网络中，毕竟我们不希望节点信息被只限制在它的小邻域中。

之前介绍的“局部和迭代”方法可以实现context diffusion。如下图所示：


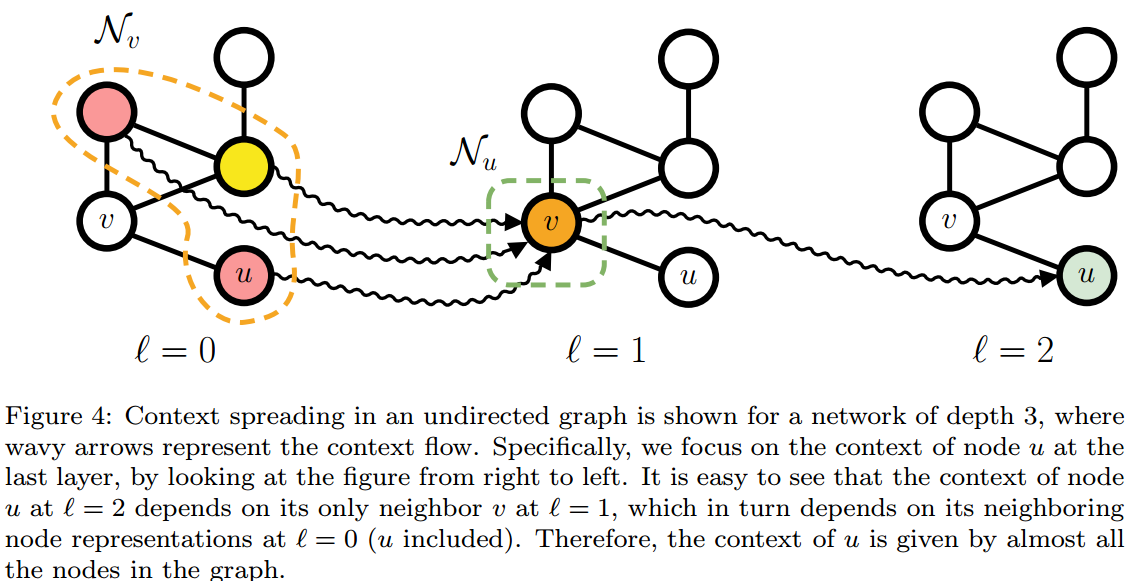
通过两层的迭代，节点\(u\)能够接收到更多节点的信息。而如果增加到第3层迭代，则\(u\)将接收到所有节点的信息。这也说明了深度不仅有助于特征的自动化处理，而且还对context diffusion。

根据context diffusion实现机制的不同，我们将DGNs的模型分为下面3类：

  • Recurrent Architectures

    代表是Graph Neural Networks（GNNs）【89】和Graph Echo State Networks（GESNs）【35】，通过在一个操作上进行反复的迭代计算来实现context diffusion。一般需要通过动力学上的限制使得在recurrent iteration的时候收敛。

  • Feedforward Architectures

    没有使用迭代，而是通过堆叠多层来实现。和recurrent architecture相比，每一层（或迭代）使用的是不同参数的layers，而且不需要有收敛的限制。

    这也是最常见的，我们接触到的大多数图神经网络都是这个。

  • Constructive Architectures

    可以看做是Feedforward architecture的特殊形式，区别在于其训练时是逐层训练的。

    好处在于这可以避免一些梯度消失/爆炸的问题，所以context可以更加有效地传递到其他节点中。并且在逐层训练时，还可以通过某些策略自动确定使用的层数。

    代表有Neural Network for Graphs（NN4G）【74】和Contextual Graph Markov Model（CGMM）【3】。

构建模块

介绍我们构建模型常使用到的模块，以及如何将这些模块进行组装构成一个模型。

邻接点聚合（Neighborhood Aggregation）

这里我们假设graphs是non-positional，所以我们需要使用permutation invariant function。

最general的形式，如下：

\[\mathbf{h}_v^{l+1}=\phi^{l+1}(\mathbf{h}^l_v,\Psi(\{\psi(\mathbf{h}_u^l)|u\in\mathcal{N}_v\})) \tag{1}\]

  • 处理graph的edges

    上面的公式并没有考虑到edges的特征。如果edges的属性是离散的（比如边的类型有2种），则我们可以将上面的公式1进行修改： \[\mathbf{h}_v^{l+1}=\phi^{l+1}(\mathbf{h}^l_v, \sum_{c_k\in\mathcal{A}}{(\Psi(\{\psi(\mathbf{h}_u^l)|u\in\mathcal{N}_v^{c_k}\})\cdot w_k)}) \tag{2}\]

    其中\(c_k\)是边的标签，\(w_k\)是该边对应的贡献度，是一个可训练的参数。NN4G、R-GCN和CGMM都实现了公式2。

    更general，针对边的特征是连续的： \[\mathbf{h}_v^{l+1}=\phi^{l+1}(\mathbf{h}^l_v, \Psi(\{e^{l+1}(\mathbf{a}_{uv})^T\psi(\mathbf{h}_u^l)|u\in\mathcal{N}_v\})) \tag{3}\]

    其中\(e^{l+1}(.)\)和\(\phi\)、\(\psi\)一样，可以是任意的函数。

  • 注意力机制

    需要给与一个注意力权重，此权重由两点的特征进行计算，可以使用下面的公式描述：

    \[\mathbf{h}_{v}^{l+1}=\phi^{l+1}(\mathbf{h}_v^{l}, \Psi(\{\alpha_{uv}^{l+1}\cdot\psi^{l+1}(\mathbf{h}_u^l)|u\in\mathcal{N}_v\}))\tag{4}\]

    其中\(\alpha_{uv}\)就是注意力权重，在GAT【102】中，其计算时没有考虑边的特征： \[\alpha_{uv}^l=\frac{\exp(w_{uv}^l)}{\sum_{u'\in\mathcal{N}_v}{\exp(w_{u'v}^l)}}\] \[\begin{aligned} w_{uv}^l&=a(\mathbf{W}^l\mathbf{h}_u^l,\mathbf{W}^l\mathbf{h}_v^l) \\ &=LeakyReLU((\mathbf{b})^T[\mathbf{W}^l\mathbf{h}_u^l,\mathbf{W}^l\mathbf{h}_v^l]) \end{aligned}\] 其中\([:,:]\)表示concatenation。另外GAT还使用了multi-head attention，即将多个注意力机制的输出concat或average。

  • 采样

    当graphs比较large或dense的时候，邻接点数目太多，就不适合将全部的邻接点进行处理，sampling是自然的解决这个问题的想法。


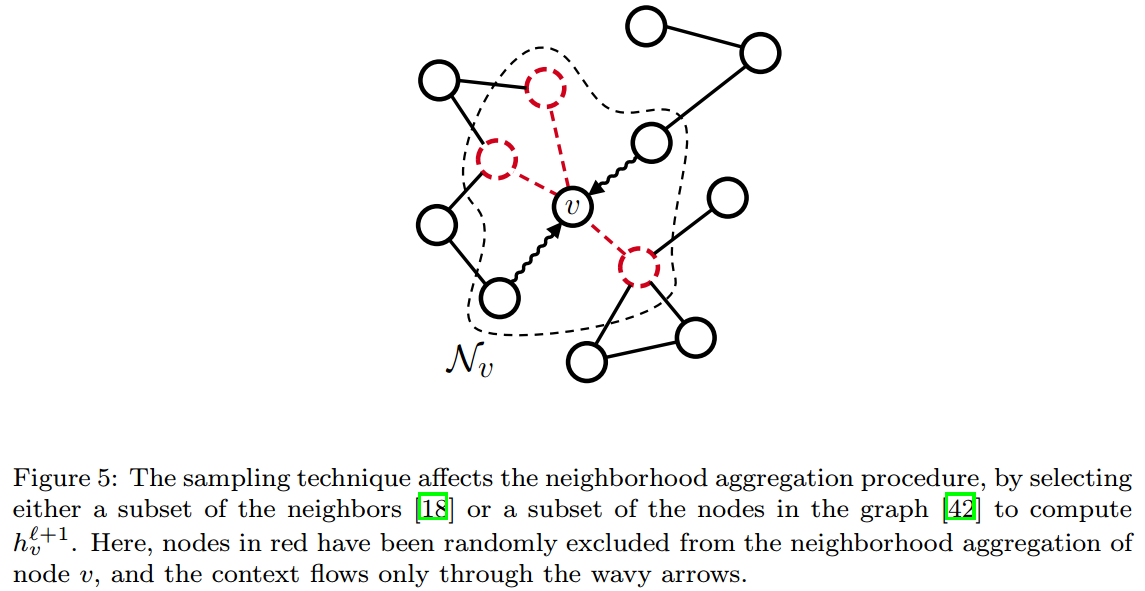
    采用这种策略的模型有FastGCN【18】和GraphSAGE【42】：

    • FastGCN：在每一层，使用importance sampling进行采样（降低方差）。
    • GraphSAGE：通过一些策略来选择本次传递信息到目标节点的节点是哪些，这些节点可能不只是目标节点的邻接点，还有可能是目标节点的二阶邻接点、三阶邻接点等。所以GraphSAGE可能不止有locally的能力。

下面的tab1列举了我们常用的进行node aggregation的各种方法，可以参考使用：


池化

pooling主要有3个作用：

  • 发现重要的communications。
  • 将communications的信息注入到学习的features中。
  • 降低计算复杂度

pooling可以分为两类：

  • adaptive，自适应

    参数化的、可学习的决定怎样进行pooling。

    DiffPool【120】，首先使用本层学习到的特征计算一个soft-membership matrix \[\mathbf{S}^{l+1}=softmax(GNN(\mathbf{A}^l, \mathbf{H}^l))\tag{5}\] 然后再使用这个matrix重新构筑graph \[\mathbf{H}^{l+1}={\mathbf{S}^{l+1}}^{T}\mathbf{H}^l\quad\text{and}\quad \mathbf{A}^{l+1}={\mathbf{S}^{l+1}}^T\mathbf{A}^l\mathbf{S}^{l+1}\] 根据你想要的保留多少个节点来设置\(\mathbf{S}^{l+1}\)的维度。因为是soft的，所以整个过程可微，同时使得经过其pooling后的graph是全连接的。

    TopKPool【37】，设置了一个可学习的projection vector \(p^l\)来计算一个scores， \[s^{l+1}=\frac{\mathbf{H}^lp^{l+1}}{||p^{l+1}||}\] 保留这个scores排名靠前的节点和他们之间的相互联系。

    SAGPool【62】则在TopKPool的基础上，使用attention score替代了projection vector \[s^{l+1}=\sigma(GCN(\mathbf{A}^l,\mathbf{H}^l))\]

    EdgePool【33】则将目标放在了边上，为边计算一个权重，权重靠前的边连接的两个节点会被融合成一个， \[s^{l+1}((u,v)\in\mathcal{E}_g)=\sigma(\mathbf{w}^T[\mathbf{h}_v^l,\mathbf{h}_u^l]+\mathbf{b})\]

  • topological，基于拓扑学的

    比如GRACLUS【22】使用谱聚类、NMFPool【2】基于非负矩阵分解等。


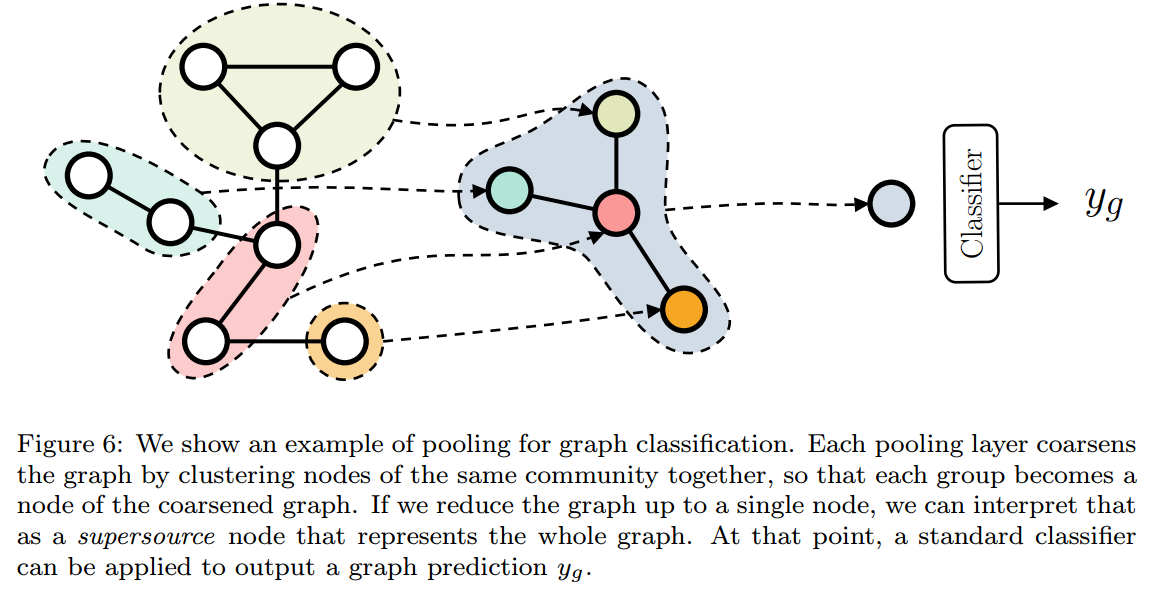
用于graph embedding的node aggregation

现在的我们的任务是得到一个graph的feature，所以需要将node features进行聚合得到graph feature，同样这个过程必须是permutation-invariant。

最常用的就是直接使用sum、max、mean等函数。【123】则进行了一些细致的研究，其先对node features进行一次MLP映射，然后进行summation，然后经过一个非线性映射完成。

至于使用那些特征来计算graph feature：

  • 最常见的是只使用最后一层的feature
  • 将所有中间层的feature都concat
  • 将所有中间层的feature看做是一个feature sequence，使用LSTM来处理【64】
  • SortPool【125】

任务

无监督学习

  • Link prediction

    试图去建立node representation，使得相邻的node之间是相似的。所以其reconstruction loss【59】可以写成 \[\mathcal{L}_{reg}(g)=\sum_{(u,v)}{||\mathbf{h}_v-\mathbf{h}_u||^2}\tag{10}\]

    另外，也可以把edge看做存在或不存在，从而构建probabilistic的formulation【58】 \[P((u,v)\in\mathcal{E}_g|\mathbf{h}_v,\mathbf{h}_u)=\sigma(\mathbf{h}_v^T\mathbf{h}_u)\tag{11}\]

    使用上面的loss，意味着你认同这样的假设：相邻的节点应该有更大的倾向被分到相同的community/class中，这称为homphily【69】。这也可以在监督学习中作为一个正则化出现。

  • Maximum Likelihood

    当认为neighborhood服从一定的分布时，我们可以使用极大似然法进行训练。一个典型的例子是CGMM【3】，其堆叠了simple Bayesian Networks，每一层有下面的likelihood： \[\mathcal{L}(\theta|g)=\prod_{u\in\mathcal{V}_g}\sum_{i=1}^CP(y_u|Q_u=i)P(Q_u=i|\mathbf{q}_{\mathcal{N}_u})\] 其中，\(Q_u\)是每个节点的隐藏类别，一共有\(C\)类别。\(\mathbf{q}_{\mathcal{N}_u}\)是节点\(u\)的所有邻接点的特征。\(y_u\)是节点\(u\)的一个特征。

    这个有点像节点分类了。

    用到类似技术的还有【83,58】的研究。

  • Mutual Information

    最大化两个相似的graphs之间的MI作为无监督学习的loss。比如DGI【103】，其先使用corruption function（就是添加噪声等扰动操作）生成一个\(g\)的扰动版本\(\widetilde{g}\)，然后训练一个discriminator来识别两个图。

  • Entropy regularization for pooling

    当使用adaptive pooling的时候，模型会趋向于将每个节点分给单个community。【120】使用了entropy loss来解决这个问题： \[\mathcal{L}_{ent}(g)=\frac{1}{|\mathcal{V}_g|}\sum_{u\in\mathcal{V}_g}H(\mathbf{S}_u)\] 其中\(H\)表示计算entropy，\(\mathbf{S}\)表示soft-cluster assignment matrix（公式5），\(\mathbf{S}_u\)表示其中表示\(u\)的那一行。

监督学习

  • Node Classification

    这里有两种类型的node classification，即：

    • inductive node classification，在一张（或多张）graphs上学习得到模型后，在一张新的graphs上进行分类。
    • transductive node classification，只有一张graph，其中有一些节点类型未知，对这些节点进行分类。

    我们会发现benchmark上的结果和实验环境的设置息息相关【93】。

  • Graph Classification/Regression

    与node相比，这里就是多了一个node aggregation的过程。

    同样的，也存在着各种实验基准不一样导致的混乱。【25】推荐了一个同一的平台来进行评价。


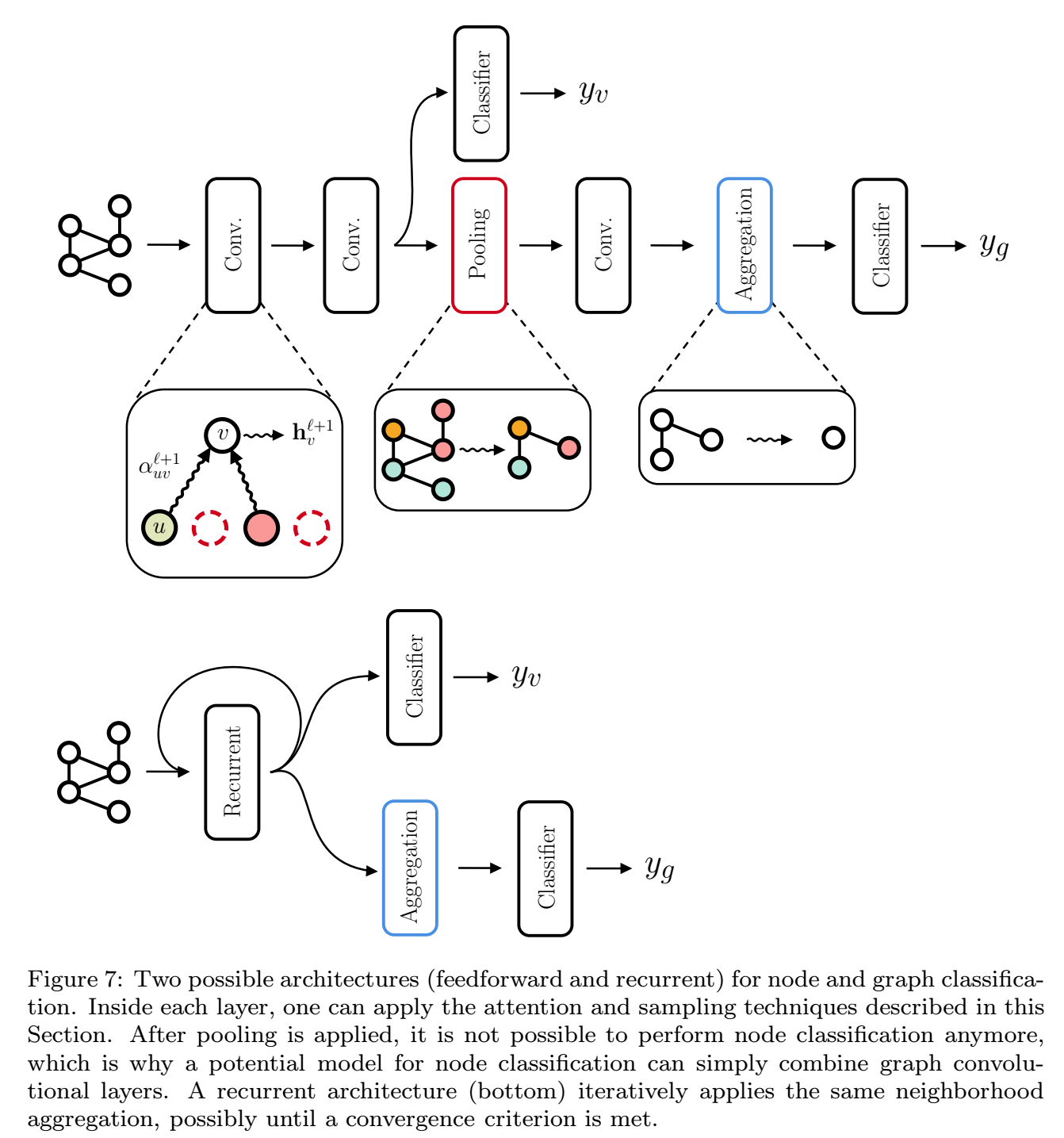
生成学习

  • Graph-level decoding

    输入一个graph的embedding，输出一个dense probabilistic的adjacency matrix \(\widetilde{\mathbf{A}}\in\mathbb{R}^{k\times k}\)，其中\(k\)表示允许最多的节点数目，元素\(\widetilde{a}_{ij}\)表示节点\(i\)和\(j\)间存在连接的概率。然后使用极大似然法进行训练： \[\mathcal{L}_{decoder}(g)=-\log P(\widetilde{\mathbf{A}}|\widetilde{\mathbf{h}}_g)\tag{14}\] 其中\(P(\widetilde{\mathbf{A}}|\widetilde{\mathbf{h}}_g)=MLP(\widetilde{\mathbf{h}}_g)\)。

    得到probabilistic adjacency matrix后，要想得到一个novel graph，有下面的3种方法：

    • 直接根据概率\(\widetilde{a}_{ij}\)进行采样
    • 在probabilistic和ground truth之间进行approximate graph matching【96,60】
    • 使用Gumbel-Softmax将采样过程可微【20】

  • Node-level decoding

    即首先我们采样得到的不是graph的representation，而是很多个node的representation。然后根据这些node的representation看是否两个nodes之间有连接： \[\mathcal{L}_{decoder}(g)=-\frac{1}{|\mathcal{V}_g|}\sum_{v\in\mathcal{V}_g}\sum_{u\in\mathcal{V}_g}\log P(\widetilde{a}_ij|\widetilde{\mathbf{h}}_u,\widetilde{\mathbf{h}}_v)\] 其中的概率可以通过公式11的方式进行计算。这样的生成过程是permutation-invaraint的，但相对来说计算量特别大。


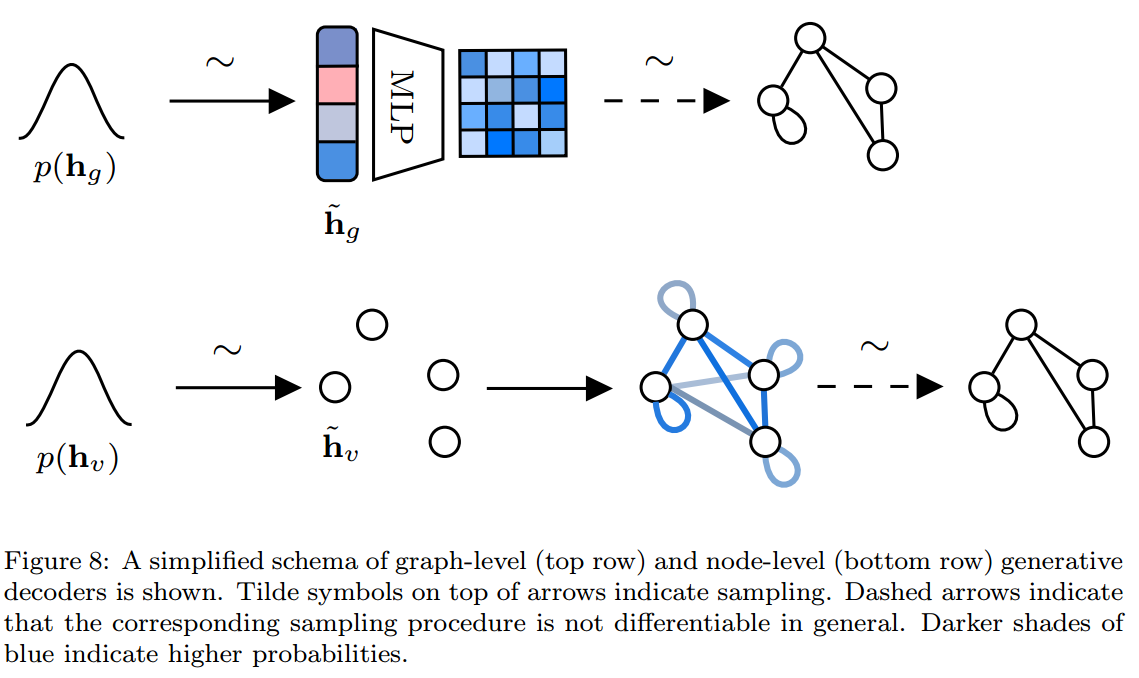
  • Generative Auto-Encoder

    不止可以进行graph generate，还能够得到graph的embedding，原理基于VAEs。公式可以表示为： \[\mathcal{L}_{AE}(g)=\mathcal{L}_{decoder}(g)+\mathcal{L}_{encoder}(g)\] 其中的\(\mathcal{L}_{decoder}(g)\)就是上面使用的loss，而\(\mathcal{L}_{encoder}(g)\)是保证latent space的distribution和某个特定的distribution之间的相似的一个“prior” regularization。 \[\mathcal{L}_{encoder}(g)=-D_{KL}[\mathcal{N}(\mathbf{\mu},\mathbf{\sigma}^2)||\mathcal{N}(\mathbf{0},\mathbf{I}))]\]

    【14】建议可以将encoder error改为Wasserstrain loss。

  • Generative Adversarial Networks

    【27】使用graph-level decoder充当G生成adjacency matrix和node label matrix，然后将这些内容送入一个discriminator中进行判断。

    【107】则使用的是node-level的decoder。

总结


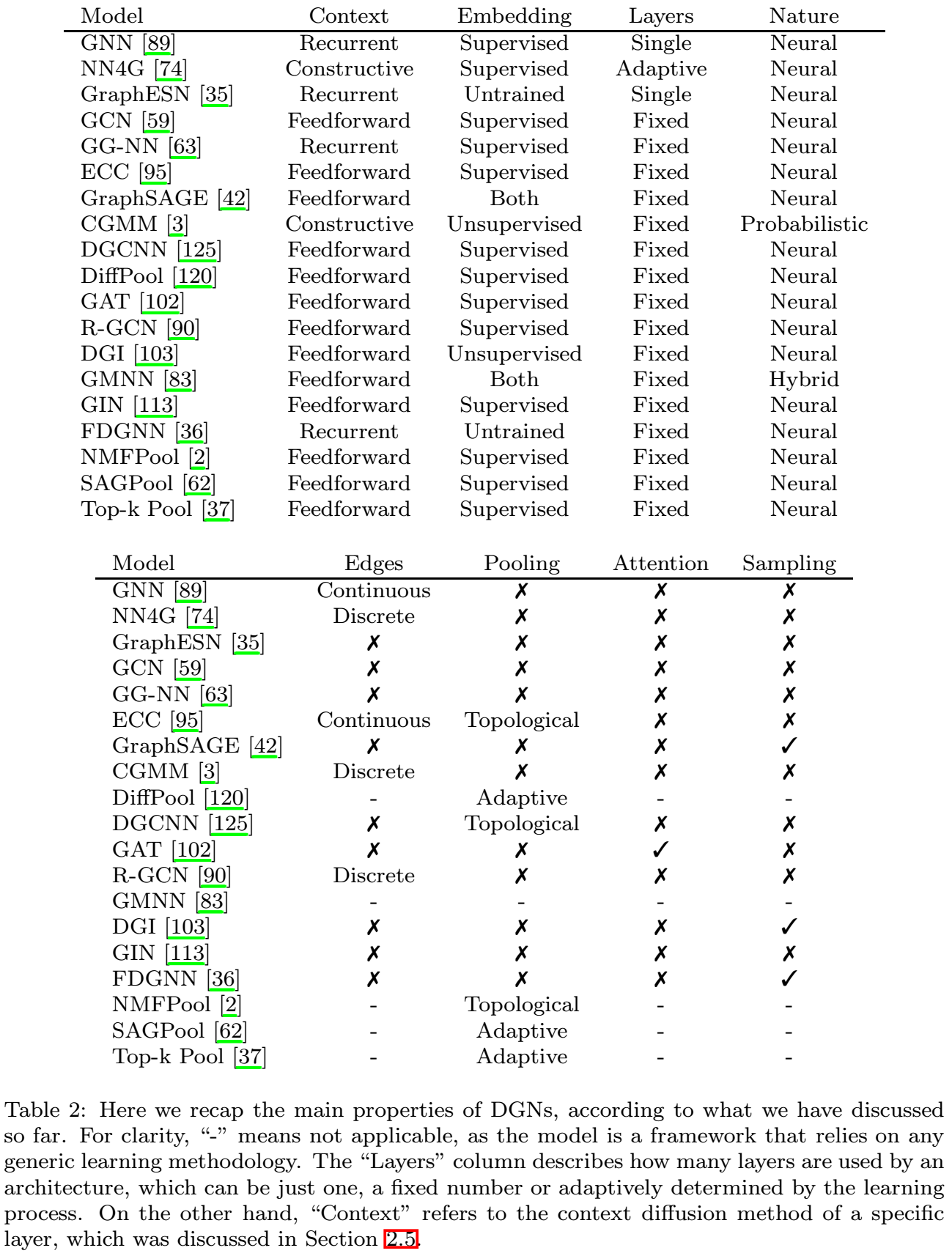
其他

还有一些主题没有被上面的分类覆盖，在这里进行简要介绍。（只关注于DL的方法，且只关注于基于“局部和迭代”策略的。）

Kernel

kernel被定义为计算一对输入间相似性的正定函数的推广形式。比如【94,84,115,31,104】即使用kernel来对graph进行操作。

kernel的主要问题在于其不是local和adaptive（自适应的），需要人类进行设计，其对于人类已经了解的性质自然非常好用，但对于其他的大量的未知，则无法触及。

基于kernel的方法一般和SVM一起来进行graph classification。

Spectral methods

Laplacian smoothing【86】、graph semi-supervised learning【81,17】、spectral clustering【105】、Graph Fourier Transform【46】、GCN【59】（是对其的一阶近似）

Random-walks

【67,104,85,50】

Node2Vec【40】、DeepWalk【82】

最近，该技术已经用来进行graph generate【12】和探索context diffusion【114】

Adversarial training和attacks

【131,28,117,54】

Sequential generative models

【65,121,5,4】

挑战

  1. Time-evolving graphs，即随时间变化的graphs，【63,110,124】等研究讨论过类似的问题。
  2. Bias-variance trade-offs
  3. 合理使用edges information，将edge informations作为context进行传播是否合理？
  4. Hypergraph learning，hypergraph指的是node set之间进行连接的对象。已经有一些研究进行了讨论【129,128,29,53】，但类似的于Time-evolving graphs，主要的问题在于缺乏数据集。

应用

这里强调，如果可以有更加通用的方法来解决（比如存在顺序等信息可以使用LSTM或CNN来解决），则使用这些方法可能是更好的选择。

化学和药物设计

  1. Quantitative Structure-Activity Relationship（QSAR）和Quantitative Structure-Property Relationship（QSPR）分析，分别是用化学结构来预测生物活动和化学性质（毒性和溶解性等）【9,76】。
  2. 化学结构相似性【24,52】。
  3. 药物设计，特别是使用生成模型来设计符合特定化学性质的分子。

以下是【25】中对一组DGNs在该领域的相关评估：


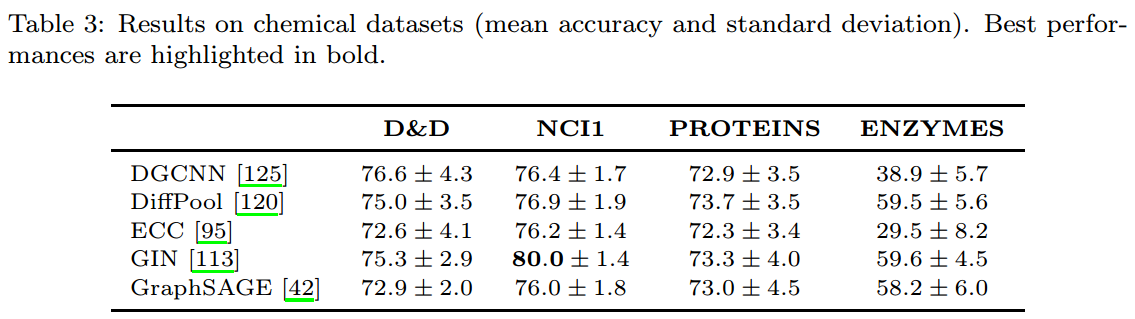
社会网络

节点是人，边表示朋友关系或共事关系，目的是检测人是否有不健康的行为或错误信息。因为隐私保护和伦理的问题，许多数据集是不公开的。

现在主要使用的节点分类的数据集有3个，【93】使用这3个数据集对常用的几个DGNs进行了评价：


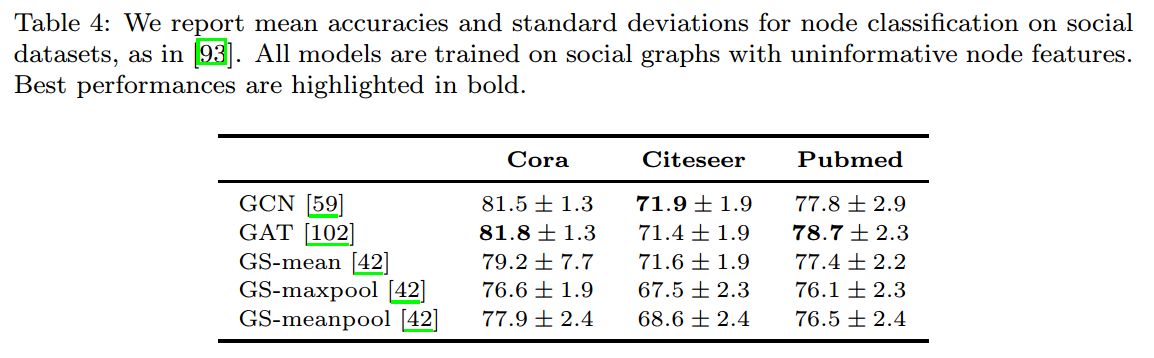
而常用的graph分类的数据集有以下5个，在常用DGNs上的结果如下:


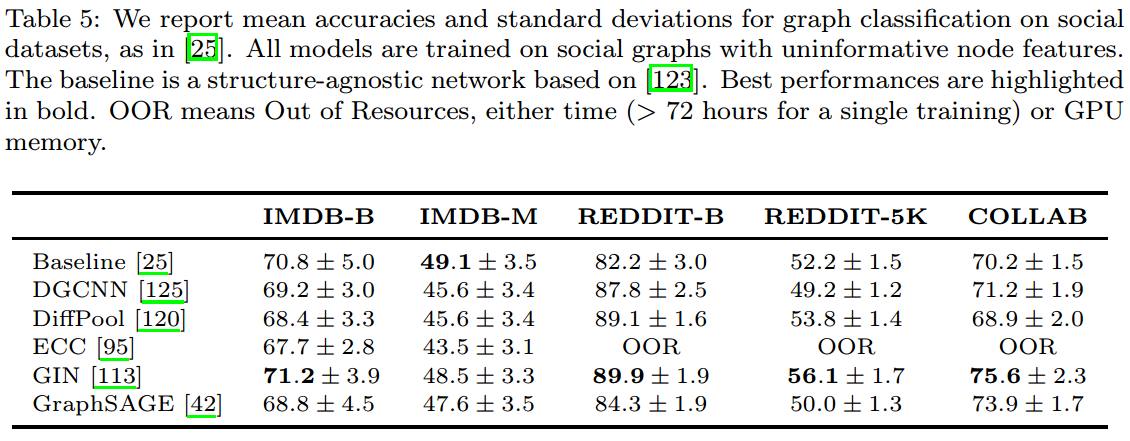
自然语言处理

将语言根据语法分解为tree，然后进行学习建模。【1,71,70,8】

安全性

静态代码分析

时空预测

道路网络的交通预测【122】、动作识别【109】、供给链任务【56】。

需要能够学习到随时间改变，graph结构的变化。

一般需要结合DGNs和RNNs。

推荐系统

这里使用的graph是用户和产品组成的一个bipartite graph。任务可以看做是link prediction，已经有些研究涉猎【78,118】。

现在主要的困难在于如何处理大型的、可伸缩的graph，一些基于采样的方法因此被提出【119】。

总结

本研究的目的不在于跟进那些最先进的研究成果，而在于将已经发表的经典进行梳理归纳。这就涉及到两个问题：

  1. 为所有的DGNs找到一个框架，【38,32,45,44】做出了自己的贡献。
  2. 为所有的DGNs提供统一的、公平的、可重复的测试平台，【25,93】认为这个工作已经迫在眉睫。

另外，PyG【30】和DGL【108】提供了DGNs的标准接口，使得我们可能轻松的实现我们的模型。

Questions

文章作者: Luyiyun
文章链接: https://luyiyun.online/2020/08/28/paper/dl/gnngentlesurvey2020/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 Luyiyun !
Deep Learning Graph Neural Networks
赏
评论
评论
  目录