Self-Attention Graph Pooling
- 杂志: None
- IF: None
- 分区: None
- Github
Introduction
CNNs在graph领域的推广的兴趣,使得出现了一些关于graph pooling的研究。
最早是一些仅仅关注于graph topology的方法:【Defferrard et al., 2016; Rhee et al., 2018】
之后开始将node features的信息考虑进去:【Dai et al., 2016; Duvenaud et al., 2015; Gilmer et al., 2017b; Zhang et al., 2018b】
最近,【Ying et al.; Gao & Ji; Cangea et al.】分别提出了几种革新的方法,使得使用GNNs来构建hierarchical representation称为可能。
然而,以上方法都存在一定的问题,有提高的空间。本研究提出SAGPool方法,其利用self-attention mechanism,并同时考虑了node features和graph topology。
Related Work
Graph Convolution
Graph Pooling
Topology based pooling
其中最常用的是Graclus【Dhillon et al., 2007】,其寻求了eigendecomposition的数学等价,从而降低了计算复杂度。
Global pooling
Set2Set【Vinyals et al., 2015】
SortPool【Zhang et al., 2018b】
Hierarchical pooling
DiffPool、gPool(更低的storage complexity)
Methods
Self-Attention Graph Pooling
这里我们使用GNNs来构建self-attention score\(Z\in\mathbb{R}^{N\times1}\),如果使用的是GCN,则公式如下:
\[Z=\sigma(\widetilde{D}^{-\frac{1}{2}}\widetilde{A}\widetilde{D}^{-\frac{1}{2}}X\Theta_{att})\]
其中\(\Theta_{att}\in\mathbb{R}^{F\times1}\),其中\(F\)是节点特征的维度。这样的scores,是考虑了features和topology的。
然后,参考gPool【Gao & Ji; Cangea et al.】的做法,设定\(k\in(0,1]\)为pooling ratio,则top \(\lceil kN\rceil\)的nodes被保留:
\[idx=toprank(Z, \lceil kN\rceil),\quad Z_{mask}=Z_{idx}\]
然后:
\[X'=X_{idx,:},\quad X_{out}=X'\odot Z_{mask},\quad A_{out}=A_{idx,idx}\]
总体来说做法和gPool一致,这在中进行过仔细介绍。
图示:
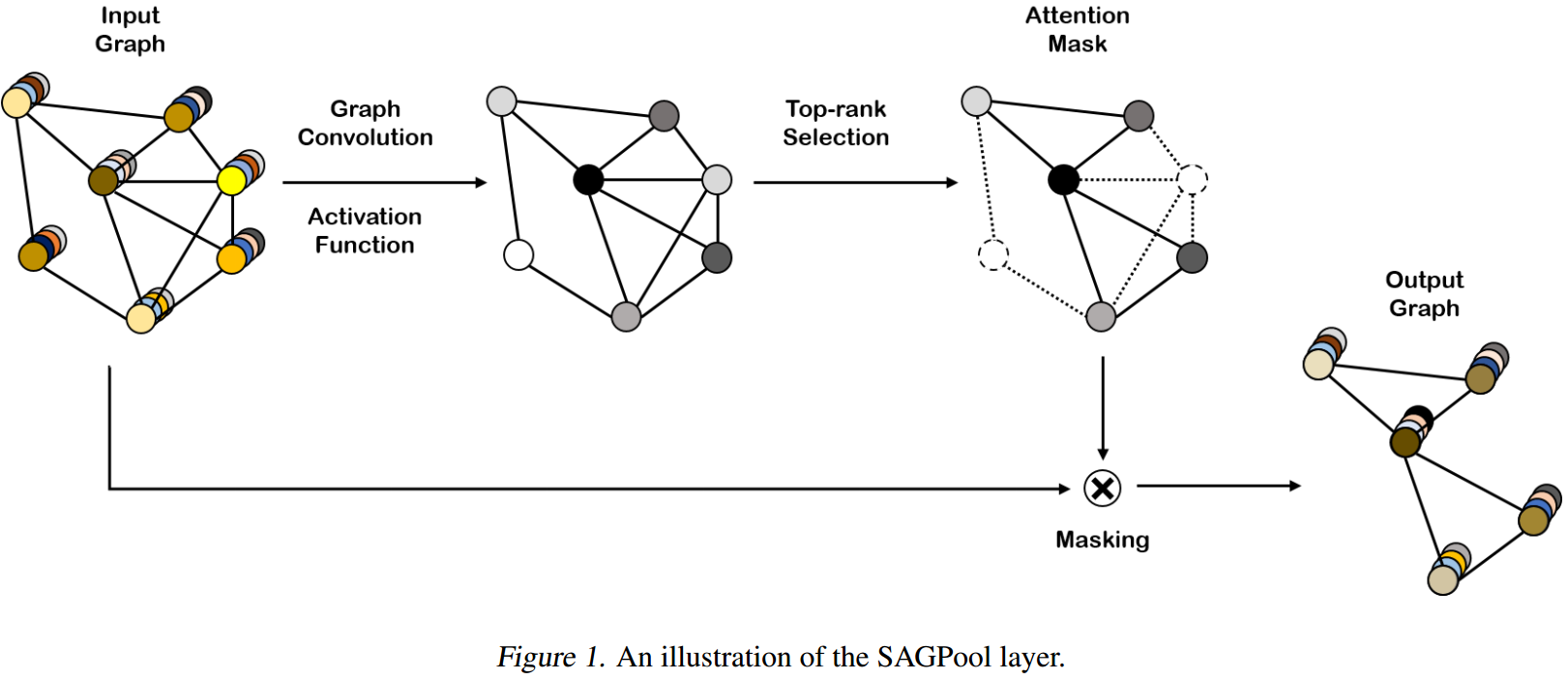
SAGpool的变体
根据上面的叙述,GCN实际上也可以换成其他的GNNs。
另外,如果我们希望在计算self-attention scores的时候考虑到2-hop neighborhoods,可以有下面2种策略:
“augmentation”
\[Z=\sigma(GNN(X, A+A^2))\]
“serial”
\[Z=\sigma(GNN_2(\sigma(GNN_1(X, A)), A))\]
另外,还可以有效下面的做法(类似multi-head):
“parallel”
\[Z=\frac{1}{M}\sum_m\sigma(GNN_m(X,A))\]
模型架构
为了便于进行比较,架构来自【Zhang et al.】和【Cangea et al.】。
convolution layer,使用GCN,激活函数用ReLU
readout layer,使用:
\[s=\frac{1}{N}\sum_{i=1}^N{X_i}||max_{i=1}^NX_i\]
也就是addition和max都考虑,并将其结构concatenation到一起。
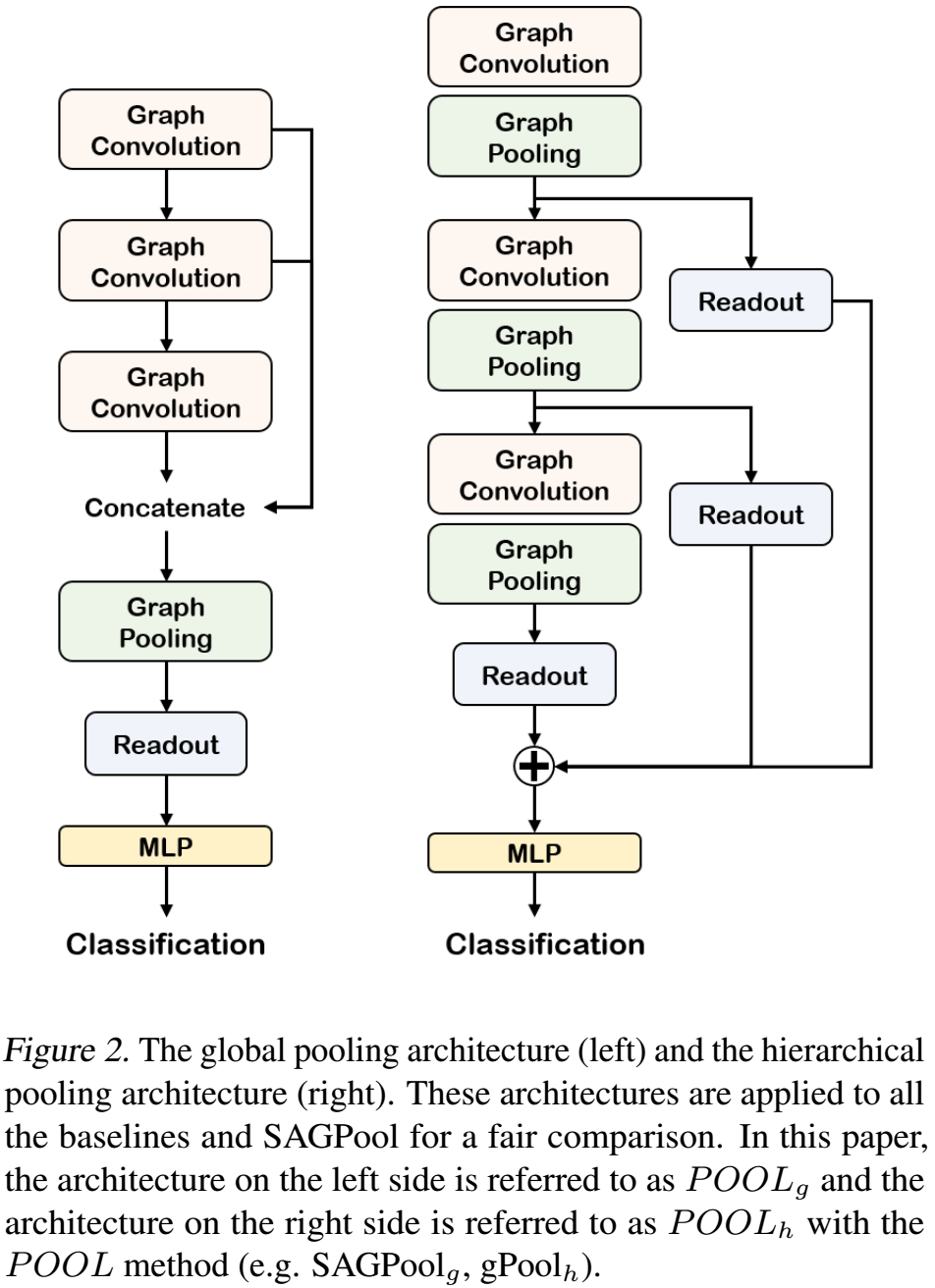
global pooling architecture
继承自【Zhang et al.】,见fig2。
hierarchical pooling architecture
继承自【Cangea et al.】,见fig2。
Results
数据集
- D&D,蛋白质分子是不是酶
- PROTEINS,也是蛋白质分子
- NCI,每张图是一个化合物,预测化合物的抗癌效应
- NCI1和NCI109
- FRANKEN-STEIN,化学分子是否是诱变剂

评价流程
进行20次10-fold CV,一共有200个testing results来得到最后的结果。training data中的10%被用来作为validation。使用Adam、early stop(50个epochs的valid loss没有降低),总的epochs是100k。
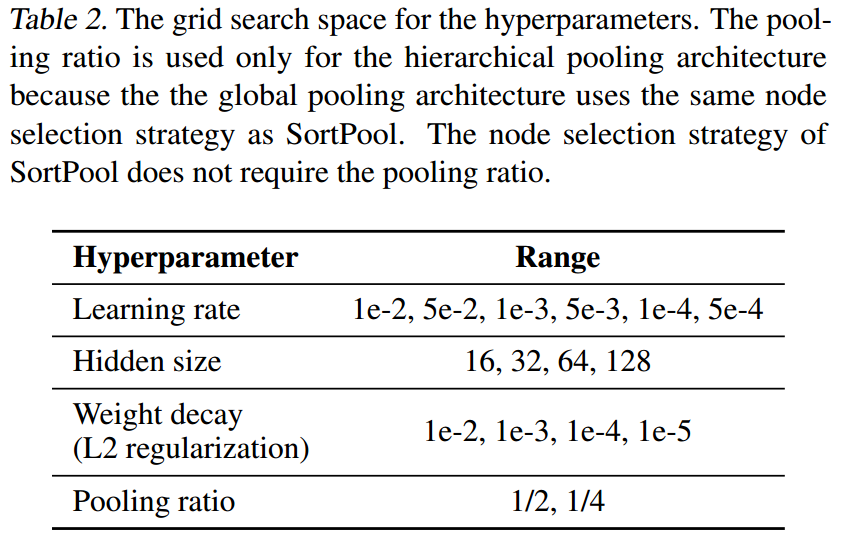
进行grid search的hyperparamters有:
基线方法
- hierarchical pooling:DiffPool、gPool、SAGPool_h
- global pooling:Set2Set、SortPool、SAGPool_g
SAGpool的变体
- 使用了3种不同的GNNs:cheb、sage、gat
- 然后是上面提到的3种变体:augmentation、serial、parallel
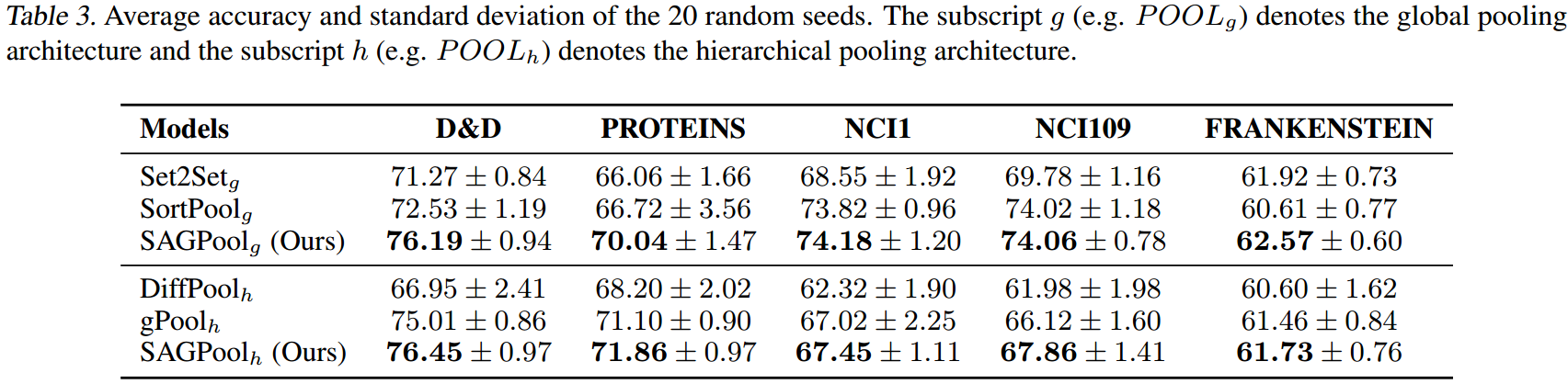
结果
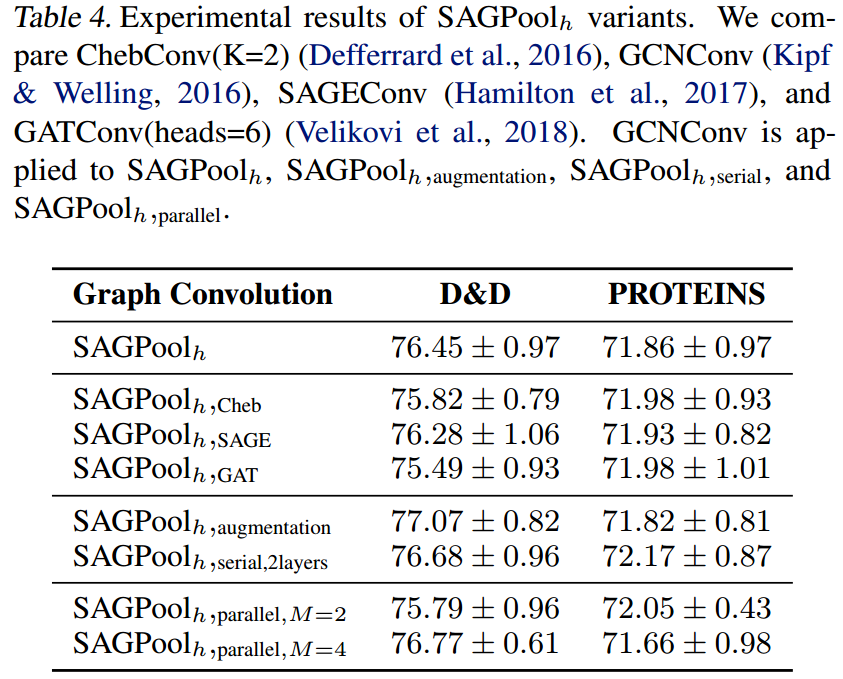
Discussion
Global和hierarchical pooling的比较
global pooling更加适用于节点数较少的graphs;而hierarchical pooling适用于节点数较多的graphs。
考虑graph topology的效果
从tab3中就可以看出,尽管SAGpool和gPool有着相同的参数数量,但效果要好得多。
稀疏实现
如果使用dense adjacency matrix进行GNNs操作,其时间复杂度和空间复杂度都要比使用sparse adjacency matrix高。SAGPool是使用sparse adjacency matrix进行操作的,而DiffPool是使用dense。
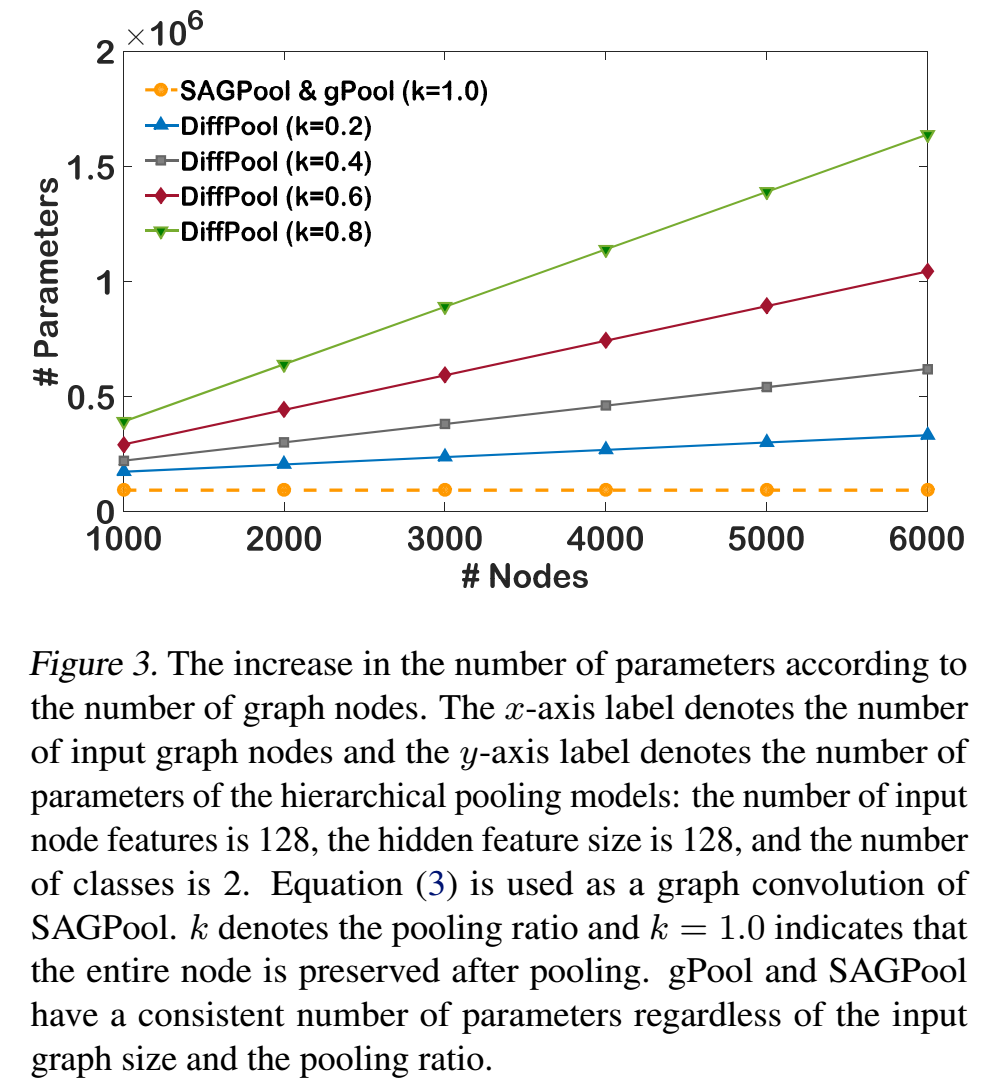
节点数量
DiffPool中参数的数量和输出的节点的数量相关,这可能导致参数的量随节点数量的线性增长,而SAGPool中参数的数量和节点的数量无关。
SAGPool变体间的比较
- 增加2-hop的关系到SAGPool中,可以提高效果。(在SAGPool中堆叠更多的GNNs)
- 使用parallel策略,选择合适的M,至少可能让结果更加稳定。
Limitations
无法确定保留节点的数量,这始终作为一个超参数。本研究试图将其变成一个2分类预测问题来自动决定哪些节点被保留,但这没有根本的解决问题。
Conclusion
未来,可以探索如何自动决定pooling size以及多个pooling layers间的相互影响。
Questions
- 在global architecture中,global pooling不就是一个readout吗?为什么会有一个pooling和一个readout分开?



