ASAP: Adaptive Structure Aware Pooling for Learning Hierarchical Graph Representations
- 杂志: AAAI
- IF: None
- 分区: None
Introduction
在使用GNNs进行graph classification的时候,学习graph-level representation是重要的。其中以hierarchical的方式来学习representation是非常有实际意义的,其可以捕捉local substructures(比如一个大分子中的分子集团)。
为了能够进行层次地学习,众多的graph pooling methods被提出:
- DiffPool,得到的assignment matrix 是dense的,无法扩展到大图。
- TopK,无法学习到足够丰富的graph structure。
- SAGPool,无法有效确定pooled graph的连通性。
本研究提出一种新的graph sparse pooling operation,叫做Adaptive Structure Aware Pooling(ASAP),来解决上面的limitations。
相关工作
GNNs
Pooling
- 早期聚焦于确定性的graph clustering algorithm【Defferrard, Bresson, and Vandergheynst 2016; Fey et al. 2018; Simonovsky and Komodakis 2017】
- pooling方法也可分为spectral【Ma et al. 2019; Dhillon, Guan, and Kulis 2007】和non-spectral的。因为spectral一般需要进行特征值分解,对于大图来说这个计算量太大,所以这里只聚焦于non-spectral的方法。
- pooling方法也可以分为global和hierarchical两种。
global pooling直接将整个graph的信息提取,相关方法有Set2Set【Vinyals, Bengio, and Kudlur 2016】、global-attention【Li et al. 2016】和SortPool【Zhang et al. 2018】。
hierarchical pooling则层次地进行节点信息的聚合,相关方法有DiffPool、TopK、SAGPool。这里注意,TopK和SAGPool都是直接将节点丢弃,其没有将节点的信息进行聚合,所以其丢失了大量的信息。
以下是几种方法的特点的总结:

Methods
因为这个方法比较复杂,这里对其进行一下总结,叙述一下其总体的思路。
首先是TopkPool的问题:
- 其在计算node score(看自己是不是重要)的时候,只考虑到自己这个节点的特征,既没有看到更大的感受野,也没有考虑到graph的结构信息。
- 在进行pooling的时候,是直接将排名靠后的节点去掉,这些排名靠后的节点的信息并没有丝毫的保留,也没有将其储存在其他的节点中。
- (自己的反驳:那我在使用TopKPool之前都先多堆叠基层GNN就好了,这些GNN理论上会解决上面的问题。)
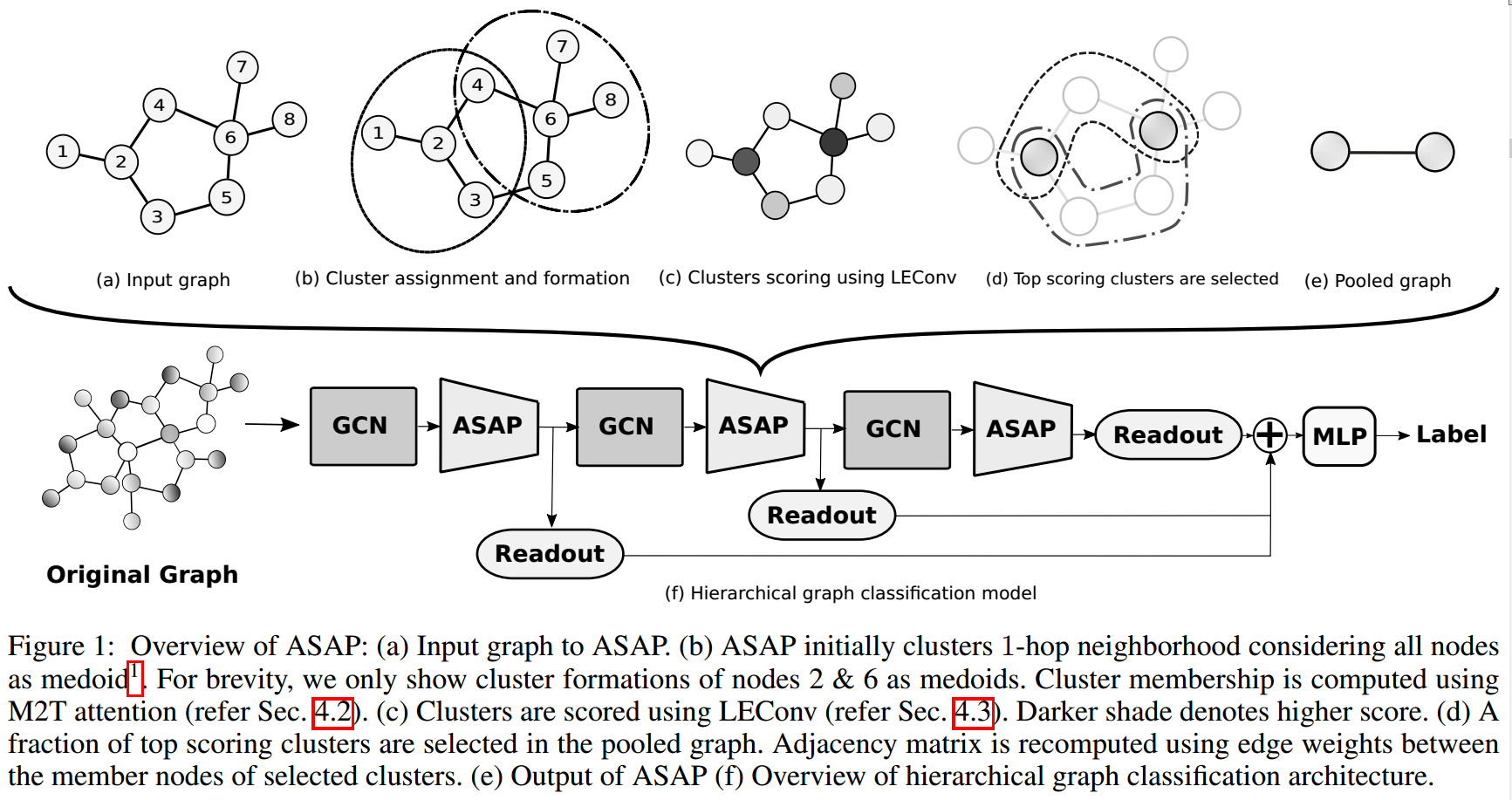
为了能够克服上面的这些缺点,ASAP进行了这些设计(思想如下图所示):
- 首先使用self-attention的架构,将每个点的邻域都看到(下图中的b),从而将这些邻域的信息都记录到这个点上去,这样得到的就是后面说所的cluster graph \(G^c\)。
- 然后根据记录的邻域信息(\(G^c\)的features matrix),使用LEConv来计算cluster score(下图中的c),然后根据这个score进行TopKPool类似的pooling操作。
- 然后根据cluster的感受野是否有重合、是否有互为邻居的点分别位于两者之中,为这些cluster之间赋予边。此时,得到的graph是\(G^p\)
自注意力
attention就是计算一个alignment score \(\alpha_{ij}\),来描述candidates \(c_j\)在query \(q_i\)上的重要性。在self-attention上,query和candidates都是input entities。根据query的选择,self-attention可以进一步分为下面两个类别:
Token2Token(T2T):candidates和query都是输入特征\(\mathbf{h}\),根据【Bahdanau, Cho, and Bengio 2014】,score的计算方式是:
\[\alpha_{ij}=softmax(v^T\sigma(Wh_i||Wh_j))\]
Source2Token(S2T):不使用query,计算方式:
\[\alpha_{ij}=softmax(v^T\sigma(Wh_j))\]
感受野
这里将感受野的概念从CNNs中推广到GNNs中。
定义pooling operation的\(RF^{node}\)为覆盖影响特点输出节点的neighborhoods所需要的hops。
定义pooling operation的\(RF^{edge}\)为覆盖影响特定输出节点的neighborhoods的edges所需要的hops。
Cluster Assignment
每个节点\(v_i\)都可以看做是一个cluster \(c_h(v_i)\)的medoid,这个cluster是该节点\(v_i\)的h hops的neighbors,即\(c_h(v_i)=\mathcal{N}_h(v_i)\)。
令\(x^c_i\)是cluster \(c_h(v_i)\)的feature representation,这时我们可以定义一个新的graph:\(G^c(\mathcal{V},\mathcal{E},X^c)\),其中的features就是cluster的features,其adjacency matrix还是原来的:\(A^c=A\)。
接下来,我们定义一个cluster assignment matrix \(S\in\mathbb{R}^{N\times N}\),其中每个元素\(S_{ij}\)表示\(v_i\)属于\(c_h(v_j)\)的“资格”。
Cluster Formation using Master2Token
接下来我们讨论如何通过self-attention来学习该cluster assignment matrix \(S\)。
基本思路就是搞一个representation \(m_i\)表示整个cluster \(c_h(v_i)\),这个就作为query。而每个cluster内的元素的表示\(x_j\in c_h(v_i)\)就是一个个candidates。
T2T和S2T都无法满足我们的要求,所以这里提出了一种新的self-attention的variant,Master2Token(M2T)。
首先,我们先使用一个单独的GCN对节点特征\(x_j\)进行一次变化,得到节点特征\(x'_j\)。这些新的节点特征包含了网络的结构信息,这在后面我们将会用到。
需要构建master query of cluster,使用下面的方式:
\[m_i = f_m(\{x'_j|v_j\in c_h(v_i)\})\]
这里的\(x'_j\)是将\(v_j\)的节点特征。
\(f_m\)可以使用\(max\):
\[m_i = max_{v_j\in c_h(v_i)}(x'j)\]
然后将master query \(m_i\)作为query,构建标准的attention模块即可:
\[\alpha_{ij}=softmax(w^T\sigma(Wm_i||x'j))\]
这里\(s_{ij}=\alpha_{ij}\),这样我们得到了cluster assignment matrix \(S\)。
注意,\(S\)并不是dense的。对于指定的节点\(v_i\),只有在其感受野内的节点(和其在\(h\) hops之内的节点)才会被赋予score。
然后计算cluster representation \(x_i^c = \sum_{j=1}^{|c_h(v_i)|}(\alpha_{ij}x_j)\)。
Cluster Selection using LEConv
类似TopKpool的思想,这里也是为每一个cluster(这是实际上是将一个感受野的信息都收集到一个节点上去了)计算一个scalar——cluster fitness score \(\phi_i\),然后选择保留前\(\lceil kN\rceil\)的cluster作为pooled graph。
这里,提出了Local Extreme Convolution(LEConv),一个新的graph convolution method可以捕捉局部的极端信息。其计算score的方式为:
\[\phi_i=\sigma(x^c_iW_i+\sum_{j\in\mathcal{N}(i)}{A^c{ij}(x^c_iW_2-x_j^cW_3)})\]
其中\(W_i,i=1,2,3\)是可学习的参数,\(\mathcal{N}(i)\)是graph \(G^c\)的第\(i\)个节点的neighborhood。
在本文的公式中,\(\sigma\)表示的是激活函数,而不是sigmoid函数。
Fitness vector \(\Phi=[\phi_1,\phi_2,\dots,\phi_N]^T\),乘上cluster feature matrix,以便上面的LEConv可以学习:
\[\hat{X}^c=\Phi\odot X^c\]
然后我们根据fitness scores来选择出前面的nodes进行保留,其他删除:
\[\begin{aligned} \hat{i} &= TOP_k(\Phi,\lceil kN\rceil) \\ \hat{S} &= S(:,\hat{i})\in\mathbb{R}^{N\times\lceil kN\rceil} \\ \hat{X^p} & = \hat{X}^c(\hat{i},:) \end{aligned}\]
其中\(\hat{S}\)是裁剪过后的cluster assignment matrix,之后还会用到。
Maintaining Graph Connectivity
根据【Ying et al. 2018】,我们可以用下面的方式来计算\(G^p\)的adjacency matrix:
\[A^p=\hat{S}^T\hat{A}^c\hat{S}\]
其中\(\hat{A}^c=A^c+I\),这保证了如何只要两个cluster有共有的节点、存在节点是邻居则就会被相连。
因为\(\hat{S}\)和\(\hat{A}^c\)都是sparse,所以这个操作是高效的。
理论分析
这里主要由3个定理构成:
GCN无法进行local extremas的学习
这里我们使用世界上的高山进行比喻理解。
我们的任务是得到一系列的代表,能够代表整个世界的高山的特征。自然的一个想法是选择世界上海拔最高的N个地点作为整个世界上高山的代表。但这里存在的问题在于,很多时候高山是一起存在的,比如青藏高原附近的海拔都明显高,如果我们单纯以海拔来选择的话,青藏高原会把世界上其他地区的高山都给挤掉。这带来了两个问题:青藏高原其实不是高山,它可以看做是喜马拉雅山附件的高地;我们这样得到的代表会只局限于局部,无法窥探整个世界的高山的特征。
用更加数学的语言来说,我们现在认为极值点可以用来描述整个graph的信息。每个极值点都可以看做是一座山。但有些山(最值点)的山坡位置也比其他极值点高,所以如果单纯进行“高度”的比较来选择,就会选择更多的点在最值点附近,无法更广的涉及到整个graph的极值点。
当使用GCN进行scores的计算,其将所有邻接点的特征进行一次weighted average的操作,所以score最高的node周围的nodes的scores也会非常高(喜马拉雅山的周围是青藏高原,最值点及其附近)。如果这个时候,我们再按照score的高低选择点的话,则我们只会选择到这个nodes及其周围,无法触及到这个graph的广泛的局部极值点信息。
而使用LEConv,因为其使用的是neighborhoods和中心节点的差值进行的学习,所以其发现极值点的能力应该是强于GCN,这里的定理就是来论述这个问题。
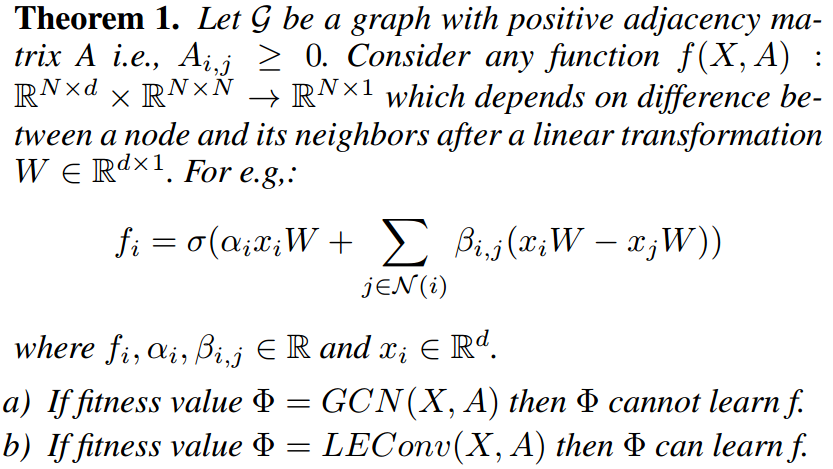
graph的连通性
这里证明了经ASAP pooling后,pooled graph拥有更好的连通性,相比于TopK和SAGPool。

ASAP是一个graph permutation equivariant操作
Results
实验设置
数据集
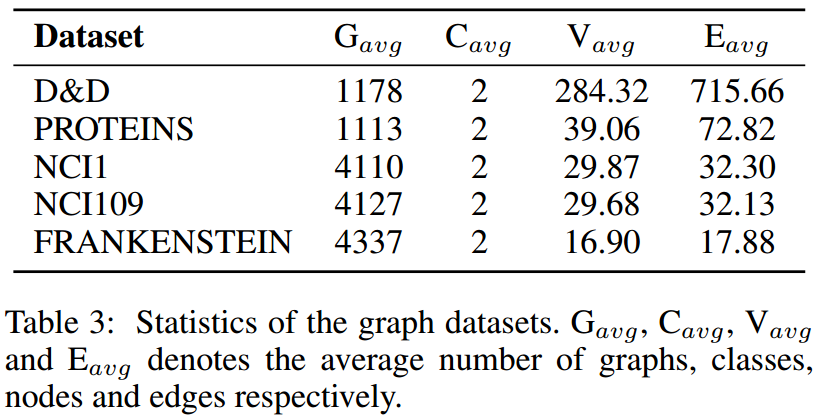
基线方法
- hierarchical methods:DiffPool、TopK、SAGPool
- global methods:Set2Set、Global-Attention、SortPool
模型设置
网络架构来自【Cangea et al.2018; Lee, Lee, and Kang 2019】,在fig1中有展示。
其中的readout是mean和max的concat(SAGPool的文章中使用过)
对于global pooling,其只在所有的GCN后使用,并且也不再用readout(global pooling本身就是一个readout)。然后各种方法有一些超参数,这些超参数会进行调整:

对于ASAP,使用\(k=0.5\)和\(h=1\)。
使用10-fold CV,然后重复20次,将200次test的结果取平均。
实验结果
在graph classification tasks上的性能比较:
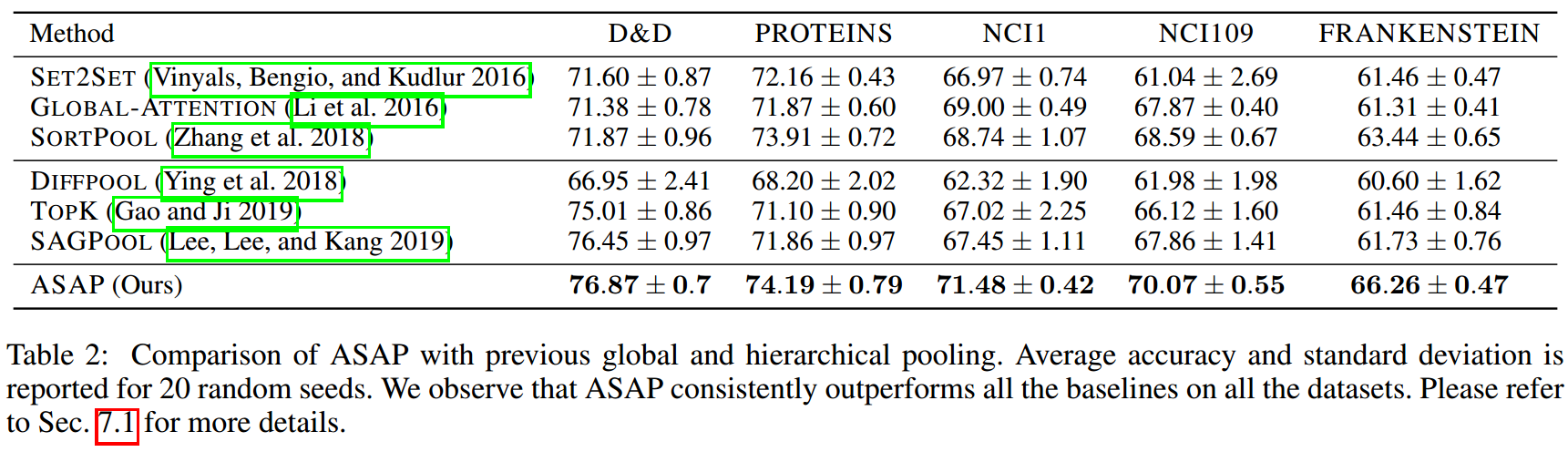
ASAP效果更好,而且训练时更加稳定。
探索“聚集整个cluster的节点特征”所产生的作用
ASAP在两个地方用到了这个:计算fitness scores和计算pooled graph的特征时
- FITNESS:表示使用了整个cluster节点的信息,否则只使用medoid的特征。
- CLUSTER:表示使用整个cluster节点的信息来更新特征,否则只是用medoid的特征作为pooled graph的特征。
则据此,我们设计了3种情形:

然后其结果如下:
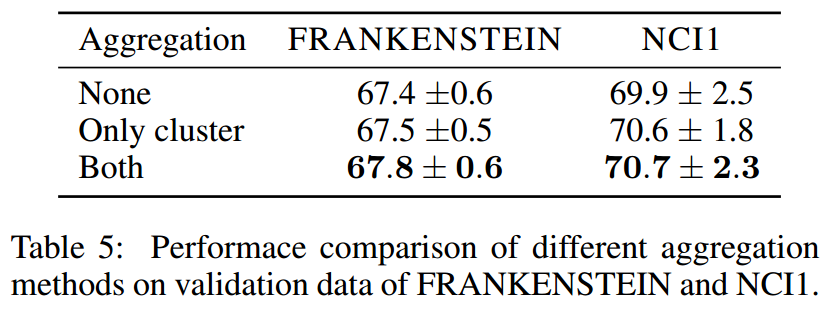
发现这种聚集cluster节点特征的方式确实对T型能的提升有帮助。
探索M2T Attention的效果
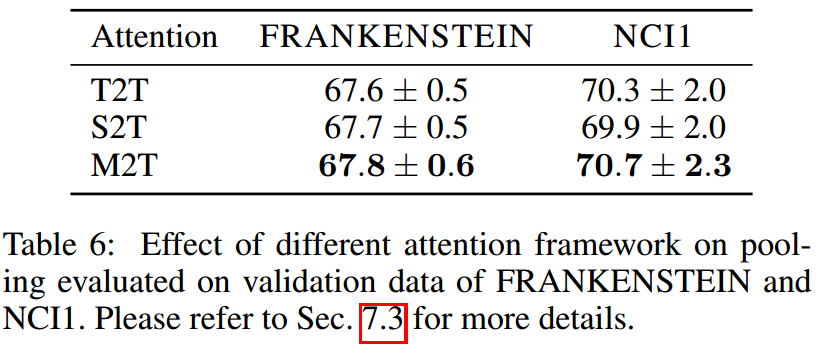
探索LEConv的效果
这里使用GCN和Basic-LEConv(3个参数矩阵都使用同一个)作为对照,效果如下:
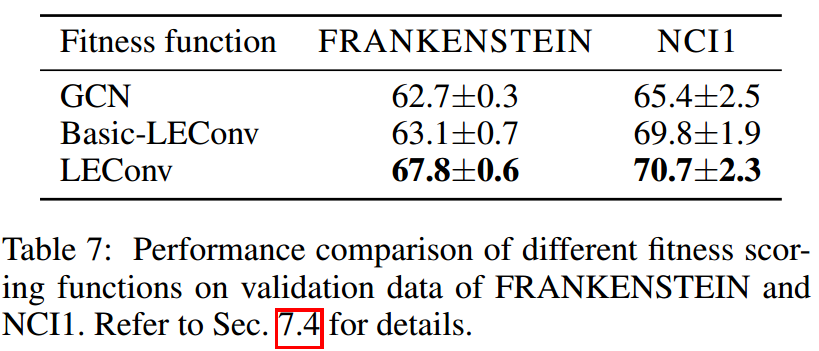
LEConv带来的提升还是很大的。
探索保留edge weights的效果

发现保留edge weights带来显著的性能提升,所以保留edge information在pooled graph上是非常必要的。
Discussion
和其他pooling方法的比较
DiffPool和ASAP都是去试图构建一个cluster,区别在于DiffPool会考虑所有的节点,而ASAP只考虑h-hop的neighborhoods。
所以DiffPool可能会导致很远的节点(拥有相似的特征)也会被聚集到一起,为了减轻这个趋势,其专门使用了一个辅助的regularization。而ASAP不需要。
DiffPool计算的cluster assignment matrix是dense的,而ASAP是sparse的。
DiffPool必须预先确定好pooled graph的节点数,而ASAP需要给出的是比例,所以更加易于操作。
TopK没有考虑到structure information,SAGPool考虑到了,但两者都没有使用cluster assignment matrix,而是直接丢弃节点,这可能造成信息的丢失。
ASAP因为构建cluster来提取cluster的信息,所以其能够捕捉更加丰富的graph structure information。
相比于TopK和SAGPool,ASAP可以使得pooled graph拥有更好的connectivity,从而更加有利于信息的流动。
另外,ASAP使用了LEConv,其保留的cluster更加合理。
self-attention变体间的比较
实际上,GAT用的就可以认为是T2T的attention。
如果我们从cluster中移除一个非medoid节点,对T2T和S2T并没有什么影响,也就是说两者都没有捕捉到cluster内部的关系。
还有一些细节,需要参考文章的appendix部分。
Questions
- \(RF^{edge}\)和\(RF^{node}\)不太懂其具体含义。



