DeepWalk: Online Learning of Social Representations
- 杂志: None
- IF: None
- 分区: None
Introduction
- 网络的稀疏性是一把双刃剑,其有益于高效离散算法的开发,但使得统计学习变得困难(【15,37,11,5,22】这些网络算法都必须解决这些问题);
- 本研究中提出了一种新的算法DeepWalk,来学习graph节点的social representation,即捕捉节点的邻居相似性和所在社区的资格信息(community membership),其灵感来源于NLP,并结合randomly-generated walks在graph上实现;
- 在Karate network(空手道网络)中的结果显示在fig1中,显示了DeepWalk得到的特征对于分类的有效性,此外在多标签的网络分类问题中也对该方法进行了测试,显示除了优于其他算法的表现,即使使用简单的logistic回归,DeepWalk的特征都表现出色;
- 本研究的贡献:
- 使用deep learning来分析图,并建立了稳健的网络结构表示;
- 在多个social networks中基于多标签分类任务对方法进行了评价,发现Micro F1都能有5%-10%的提升,甚至在某些情况下能够减少60%训练样本的使用;
- 展示了DeepWalk方法的可扩展性,并描述了如何对方法进行进一步的改进;

相关工作
本研究和其他研究的不同:
- 学习潜在表示,而不是计算统计特征【12,41】;
- 不去试图去扩展分类模型【37,20】;
- 只需要局部信息,而其他方法需要全局信息【16,39,41】(即可以在线学习);
- 将无监督学习用于graph
关系学习
- 比较著名的,比如pagerank等技术来将graph的信息进行整合;
- 还有Graph kernel【42】,但其非常慢;
- 【12,16,39-41】;
无监督特征学习
【17,3,9,21,7,6】;
Methods
问题定义
- \(G=(V, E), E\in(V\times V)\), 定义带有节点特征和节点标签的图为 \(G_L=(V,E,X,Y),X\in\mathbb{R}^{|V|\times S},Y\in\mathbb{R}^{|V|\times|Y|}\)。
- 一般上述问题被称为relational classification(collective classification),传统解决方法是使用无向Markov网络来建立模型,并使用近似推理方法(迭代分类【31】、Gibbs抽样【14】、标签松弛【18】)来计算标签的后验分布概率;
- 本研究的思路则是先去学习每个节点的表示\(X_E\in\mathbb{R}^{|V|\times d}\),其包含了X和graph结构的信息,然后再使用这些特征进行分类,这避免了迭代模型中出现的cascading errors问题【33】,并且其可扩展性也更强(易于和简单的机器学习方法进行结合);
什么叫做cascading errors问题?
社会表示学习
我们希望学习到的social representation有以下的性质:
- Adaptability:能够根据新的关系进行学习,并且不会重复之前的学习;
- Community aware:网络中节点间的social similarity应该在学习到的representation中有所表示;
- Low dimensional;
- Continuous:这可以得到更可靠的分类;
随机游走
- 定义在节点\(v_i\)上的random walk为\(W_{v_i}\),其是一个随机过程,拥有随机变量\(W_{v_i}^1,\dots,W_{v_i}^k\),其中\(W_{v_i}^{k+1}\)是这个随机过程中第\(k\)步节点随机选择的邻居节点,\(W_{v_i}^0=v_i\)。
- 该方法可以用来进行相似度度量【11】和community detection【1】,也可以用来计算灵敏度【38】;
- 本方法使用random walk来生成stream来描述这个节点的信息,这带来了2个优点:
- 可以轻松并行化;
- 基于从short random walks得到的信息,是没有必要关注到全局的,所以对图进行的更新后,没有必要从新开始训练;
连接:幂率
如果度分布服从幂律分布(scare-free),则在short random walk中节点出现的频率也是服从幂律分布的;
无标度网络的特点即大多数节点只和很少的节点相连,而有极少数的节点和很多节点相连,即随机抽取一个节点,其度为\(k\)的概率是\(P(d=k)\propto k^{−r}\),一般这个\(r\)的值在\(2-3\)之间。这个特点使得无标度网络对意外故障有强大的承受能力,而面对协同攻击时显得脆弱。
自然语言中的词频率拥有类似的分布(fig2),所以本研究希望将建模自然语言的技术用于网络;

语言模型
语言模型一般来建模在语料库中出现特定词的概率,即给定一个词序列\(W_1^n=(w_0,w_1,…,w_n)\),然后最大化\(Pr(w_n│w_0,w_1,…,w_{n−1})\);
将random walk类比为词序列,然后也来最大化相似的似然\(Pr(v_i│v_1,…,v_{i−1})\),来学习一个latent representation。其中representation使用一个函数\(\Phi:v\in V\to \mathbb{R}^{|V|×d}\)得到,最终可以表示为\(Pr(v_i│\Phi(v_1 ), …, \Phi(v_{i−1}))\);
进一步对上述方法的拓展为NLP带来了曙光【26,27】:
- 首先,不使用上下文来预测单词,而是使用单词预测上下文;
- 上下文是该单词左右(可能不止每侧一个)的单词;
- 去除了顺序的影响,直接最大化上下文中所有单词的概率,而不需要offset;
最终,得到模型: \[\max_{\Phi}{\log Pr(\{v_{i-w},\dots,v_{i-1},v{i+1},\dots,v_{i+w}\})}\]
这些扩展对于graph representation学习非常有用:
- 没有offset使得模型可以有效捕捉random walk带来的"近距离"感;
- 这样可以一次训练一个节点,容易加快训练速度;
这里我们可以看到,拥有相似邻接点的特征会拥有相似的表示;
算法
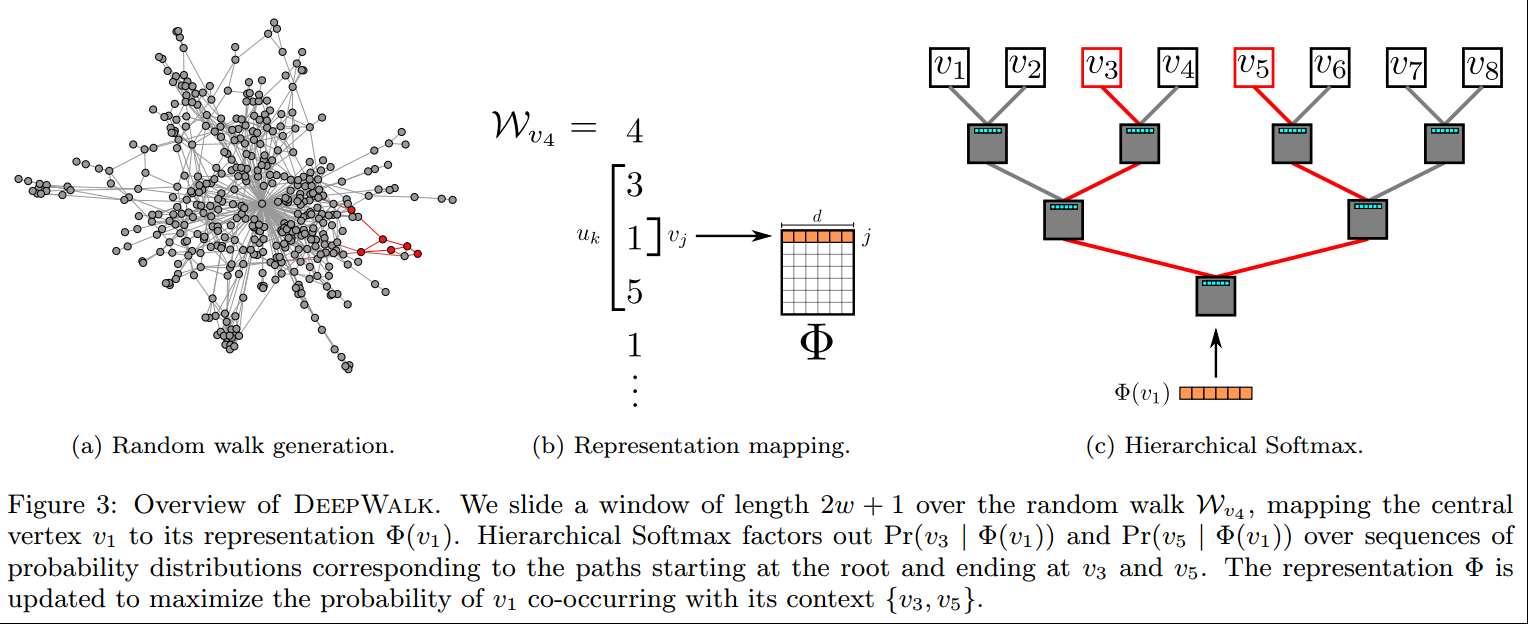
DeepWalk
Random walk generater:
这里有两个超参数需要调整,即random walk的长度\(t\),一共需要几轮random walk \(\gamma\),相应的有两个嵌套的循环;
外部的训练次数是\(\gamma\),random walk的总轮数\(S\)(pass),可以认为是epoch数,即每pass对每一个节点都random walk一次,相当于得到了一个\(|V|\times t\times S\)的数据矩阵,然后使用这个矩阵来训练,和正常的SGD过程一样,每次得到上面的矩阵的时候,都会先把节点的顺序都shuffle一遍,这样一般loss会降的快,而且泛化能力更强;
内部的训练可以认为是batch,但这里是batch size=1,即每一次都用一个点的random walk来更新参数,这里使用的是SkipGram模型来作为\(\Phi\),另外长度\(t\)不必是固定的,因为可能会回到root node,所以如果决定回到root就停下,则得到的序列长度就不是固定的\(t\),但这并不会有大的影响;

Update procedure(SkipGram):
其具体算法见algorithm2。
这里有个超参数\(w\)需要调整,对每个节点的每个\(w\)窗口内的所有其他节点,使用该节点的特征进行softmax预测,然后进行一次参数更新,这里一共进行了\(2wt\)次参数更新;
这里唯一一个问题在于,预测的节点分类数量太多,所以不能使用传统的方法来进行计算,需要使用层次softmax【29,30】来近似概率分布;
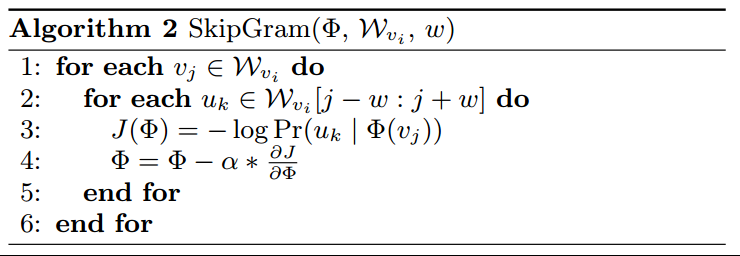
Hierarchical Softmax:
因为需要进行分类的类别数实在太多(比如有10000个分类),则softmax的分母需要加10000次\(\exp\),这无疑会增加计算量以及计算的难度;
层次softmax的想法是将多个分类概率使用多个二分类的乘积的形式来近似表示,则对于10000分类的问题可以简化为log10000个乘积运算,使得计算称为可能;
但实际上这只是一个近似,这样的方式并不能得到所有的可能的概率模式;
为了进一步加快速度,可以使用Huffman coding进一步进行加速;
Optimization
我们需要优化更新的部分有两个,一个是\(\Phi\),一个是计算层次softmax是使用的二叉树\(T\);
使用SGD进行训练,初始学习率是2.5%,之后根据看到的节点的数量进行线性的衰减;
并行训练:
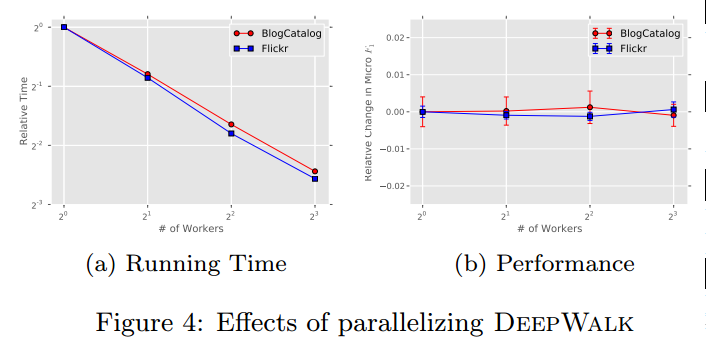
因为是幂率分布,即大多数参数的更新都是稀疏的,所以使用ASGD会更快,而且实验(fig4)显示其也没有造成性能的丢失;
算法变种
这里对上面介绍的算法进行了一些变种,来研究算法的性能
Streaming
我的理解:直接从某个节点开始random walk,然后并不停下。这样会形成一个无限长的节点序列,然后使用\(w\)的窗口来进行SkipGram训练,这另外带来了两个训练上的改变:
- 学习率是固定的,不会根据看到的节点数量进行改变;
- 没有必要每次SkipGram训练都重现建立一颗tree,直接在最开始的时候建立一颗最大的tree来分配即可;
Non-random walk:有些图上的节点本身就是有顺序的,则我们直接使用这个顺序形成序列;
Results
数据集
- BlogCatalog【39】:博客博主形成的社会网络,节点类别表示的是其博客的类型;
- Flicker【39】:照片共享网站上用户的关系网络,节点类别表示的是用户的兴趣组,比如黑白照片;
- YouTube【40】:YouTube上的用户关系网络,节点类别表示的用户喜欢的视频类别;
这些数据中节点是没有特征的,和我们普通的machine learning任务进行类别,每个节点可以看做是一个样本,但样本间不是独立的,每个样本只有标签,希望使用这些样本间的关系进行学习。
基线方法
SpectralCluster【41】:使用图的归一化Laplacian的最小的\(d\)个特征向量来得到特征矩阵;
Modularity【39】:使用图的模块化矩阵的前\(d\)个特征向量;
EdgeCluster【40】:使用k-means去聚类邻接矩阵,其相比于Modularity的优点是不需要进行矩阵分解;
wvRN【24】:即使用某个节点的邻接点该类别的概率的加权求和来计算这个节点该类别的概率:
\[Pr(y_i|N_i)=\frac{1}{Z}\sum_{v_i\in N_i}{w_{ij}Pr(y_j|N_j)}\]
Majority:直接统计训练集中每个类别的节点数目;
多标签分类任务
首先从图中随机采样出training,剩下的是test,这个过程重复10次,计算micro-F1和macro-F1的均值。
- Micro-F1先分别计算TP、FP、TN、FN,在根据公式计算F1。
- Macro-F1是先对每一类计算F1,然后计算其平均。
所有的方法使用的分类器都是one-vs-rest的logistic regression,DeepWalk的参数是\(\gamma=80,w=10,d=128\),其他方法使用的维度是\(d=500\)。
BlogCatalog:训练集比例从0.1-0.9,结果见下表,只有SpectralClustering有一定的竞争力,但在较少训练集的时候其也比不过DeepWalk;
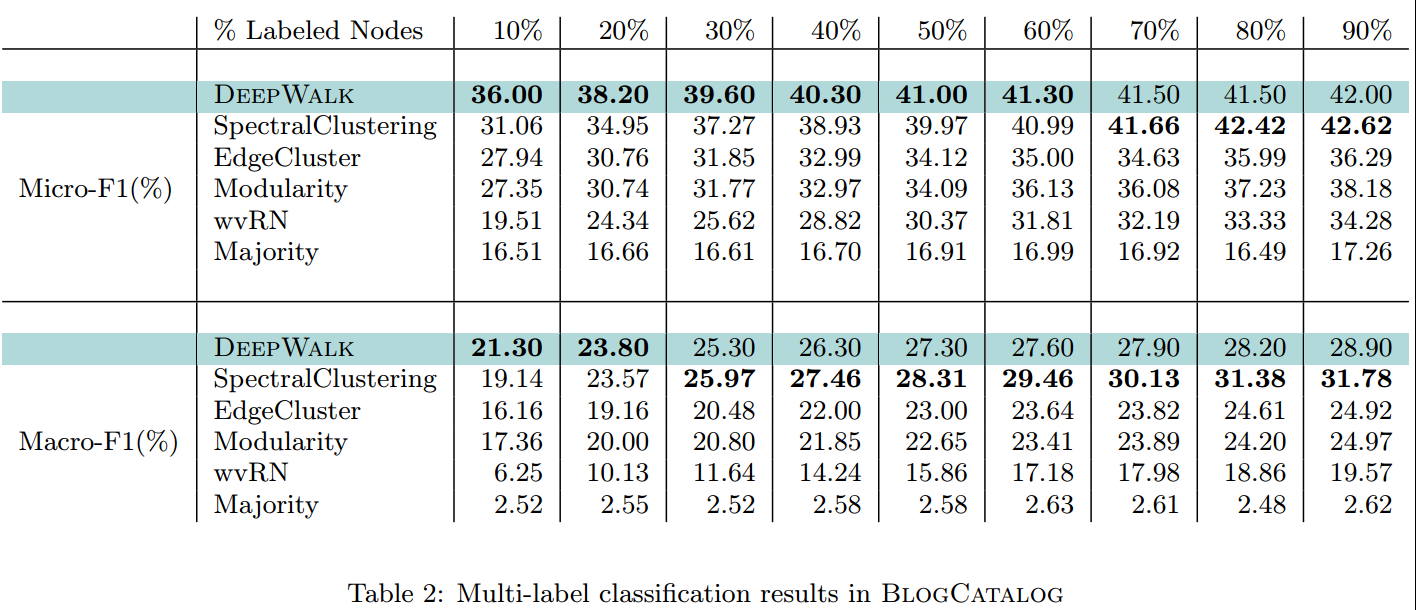
Flickr:训练集比例从0.01-0.1,看到特别是在极小训练样本的情况下,DeepWalk的效果是极好的;
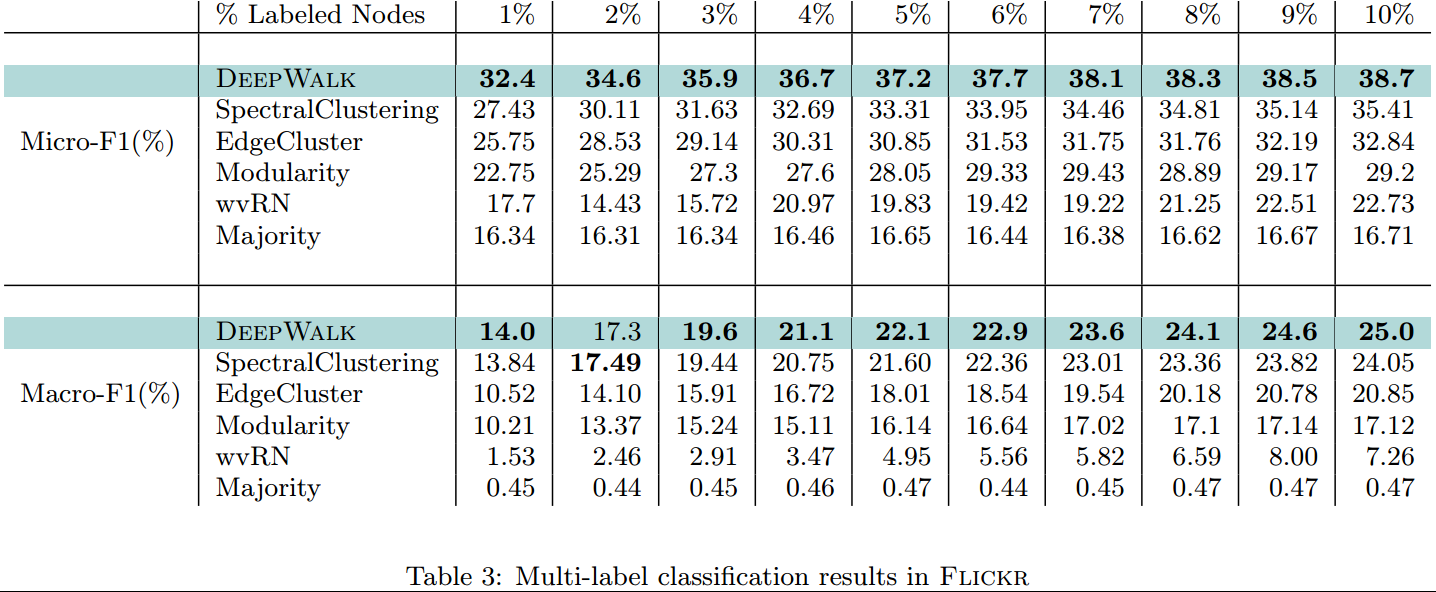
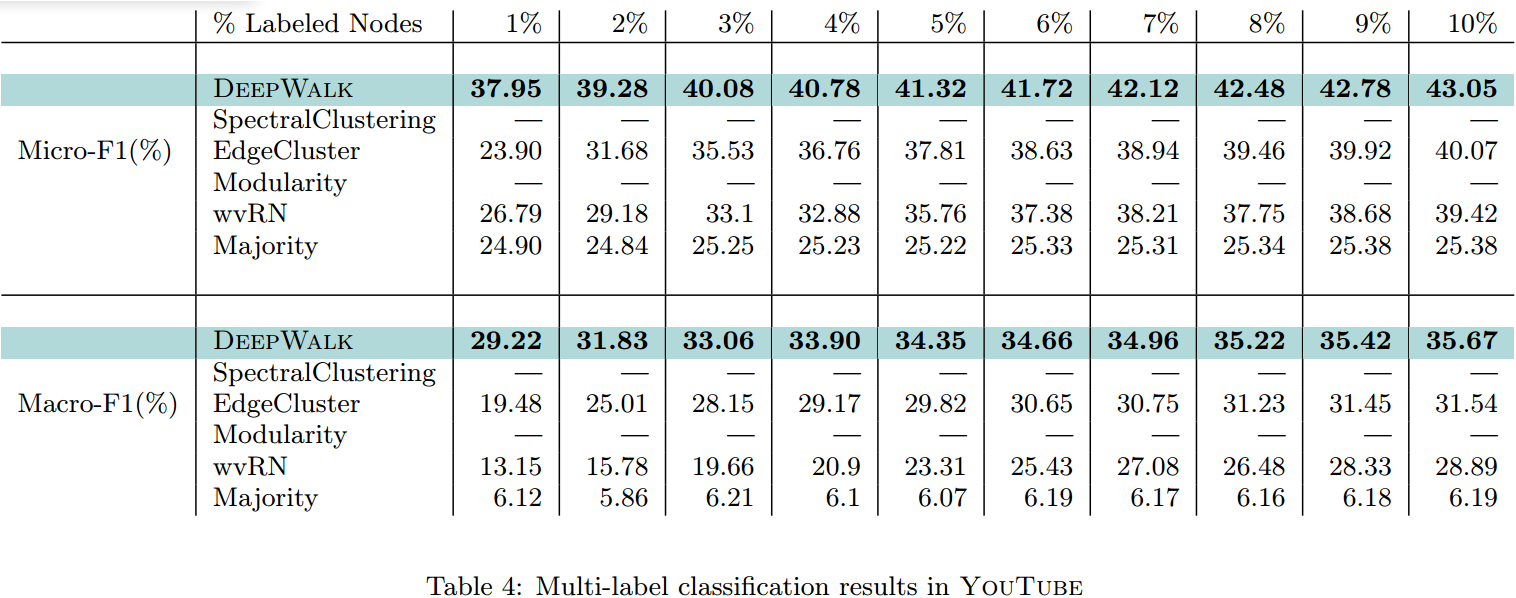
YouTube:训练集比例从0.01-0.1,因为太大,一些基线方法无法计算,发现DeepWalk方法远远好于其他方法,特别是在极小样本量的情况下(0.01);
参数灵敏度
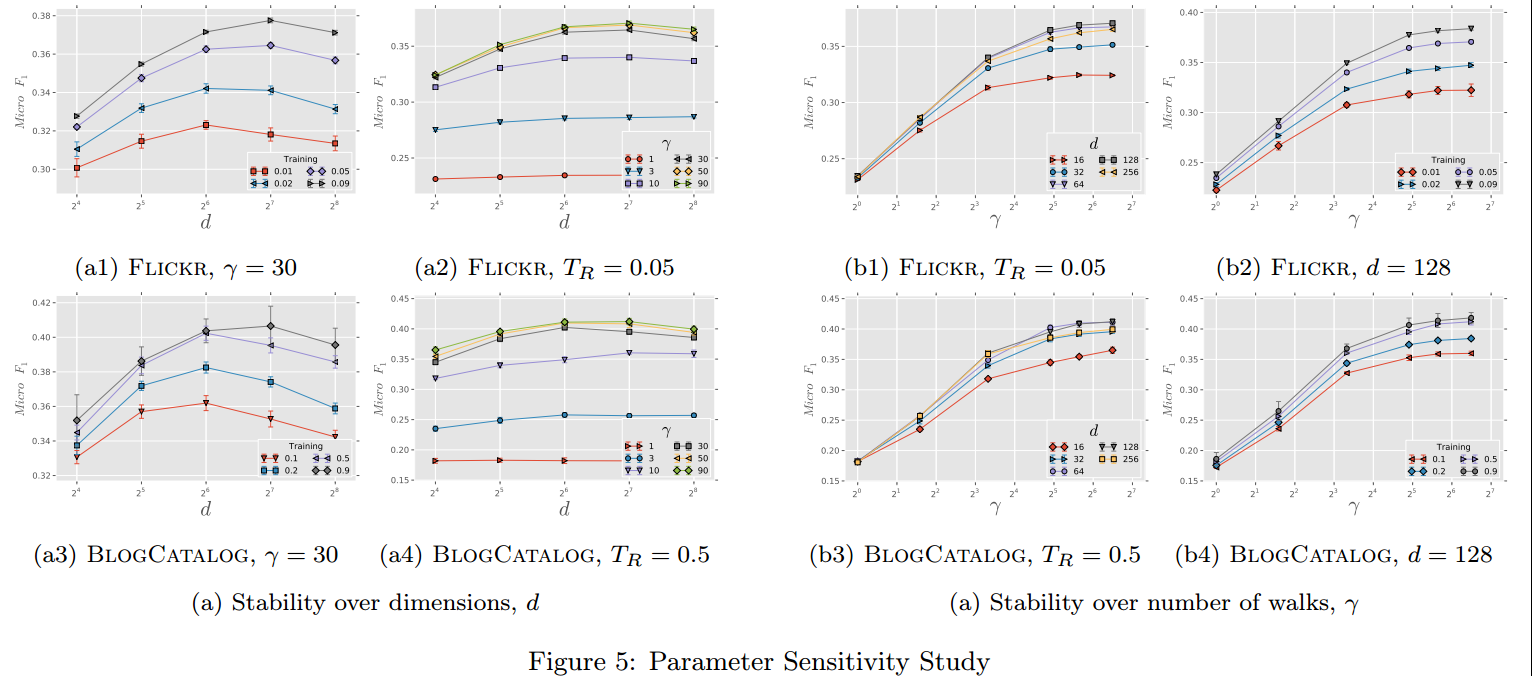
探索改变其超参数,对算法性能的影响,其中\(w=10,t=40\)是固定的,改变的是维度\(d\)、pass数量\(\gamma\)、训练集大小;(fig5)
- 维度的影响:
- 最佳的维度数会受到训练集大小的影响;
- 对于\(\gamma\)的改变,DeepWalk是稳健的;
- \(\gamma\)的影响:
- 增加\(\gamma\)会对结果有影响;
- 但随着\(\gamma\)的增加,影响逐渐有限;
- 仅需要少量的random walk,即可以学习到有效的潜在表示;
下面是并行化对运行时间和性能的影响:
Conclusion
- DeepWalk可以成功在大的graph上运行,而且性能显著优于其他为了sparse设计的算法;
- 因为利用了NLP中的知识,所以NLP中的发展也可以促进DeepWalk的提升;
- 未来会进一步研究该方法的理论依据。



