Attention Is All You Need
- 杂志: nips
- IF: None
- 分区: None
Introduction
RNN、LSTM【12】、GRU【7】是当前进行sequence建模的最优模型,【31,21,13】进一步对其进行了推广和构建基于此的encoder-decoder模型。
当使用上述模型时,一个挑战在于无法并行化,从而拖慢了训练和运行的速度。
Attention机制正在兴起【2,16,22】,但这些研究中还是将其与其他模型融合使用。
本研究中,我们完全使用attention机制,构建了一种新的架构——Transformer,其可以并行化的运行,并在非常短时间的训练后就得到了超越的效果。
背景
构建并行化的序列模型,之前的工作【20,15,8】大多采用CNNs。但其存在的问题是,难以建立距离非常远的两点间的关系。
而Transformer没有此问题。尽管attention weighted sum降低了有效的分辨率(损失了信息),但这可以通过使用multi-head attention来进行弥补。
self-attention机制已经在许多任务中表现惊人【4,22,23,19】。
end-to-end memory networks是基于recurrent attention机制的,已经在一些简单的语言问题上被证明有着不错的效果【28】。
Methods
Encoder-Decoder架构
整个模型使用encoder-decoder架构【5,2,29】。
其接受输入\((x_1,\dots,x_n)\),将其转换为连续的表示\(\mathbf{z}=(z_1,\dots,z_n)\)。给定一个\(\mathbf{z}\),decoder生成一个输出序列\((y_1,\dots,y_m)\)。进行生成的时候,模型是auto-regressive,即将上一次的结果作为输入来生成本次的输出。
整个模型可以有下面来的图来表示:
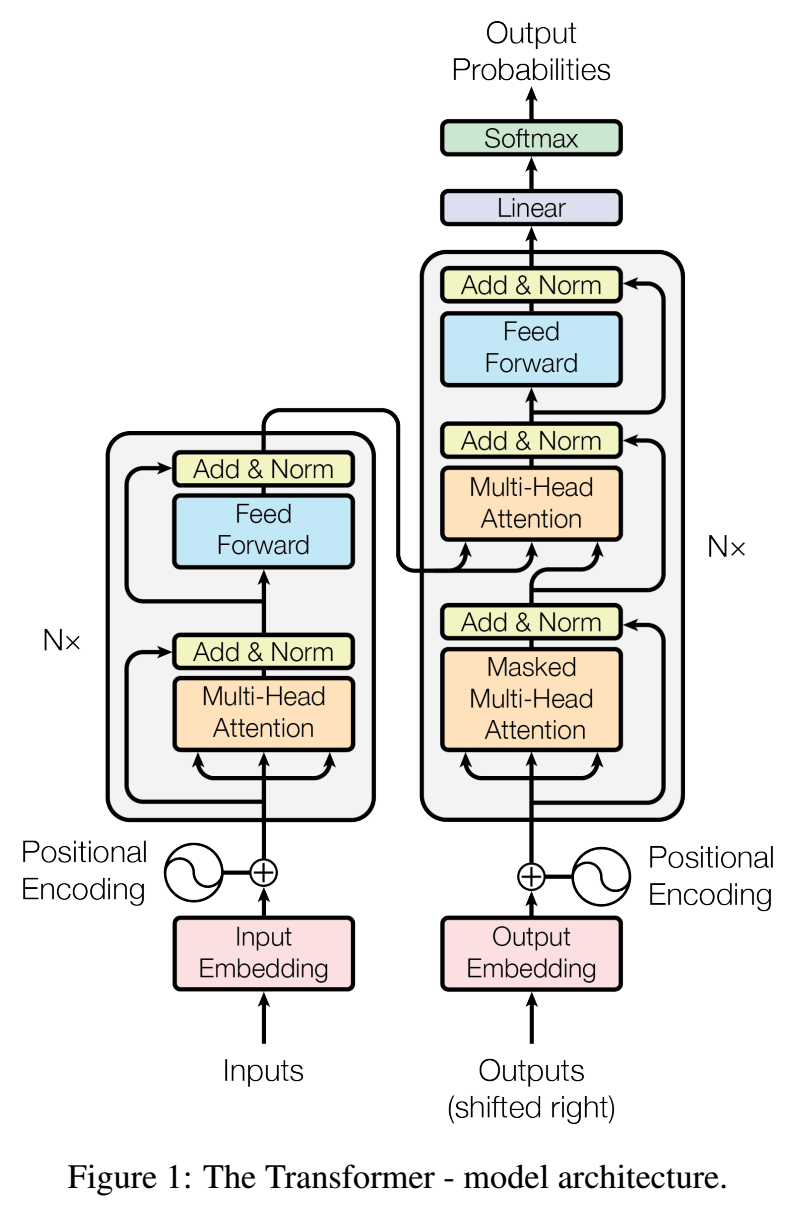
Encdoer:
encoder堆叠了6个相同的layers。
每个layer有两个sublayers堆叠而来:
- 第一个是multi-head self-attention
- 第二个是一个简单的fc layer
每个sublayer都有残差连接,并且之后再跟上一个layer normalization【1】(\(LayerNorm(x+Sublayer(x))\))。
为了方便使用残差连接,hidden layer units都是512。
Decoder:
decoder也是堆叠了6个相同的layers。
每个layer除了encoder有的2个sublayers外,还插入了另外一个sublayers。这个layer是一个相同的multi-head self-attention,其接受encoder的输出,混合decoder的输入从而生成序列。
decoder只能看到前面的东西来生成后面元素(我们要保证自回归特性成立)。所以,decoder的输入需要先mask掉后面的内容(后面会说到,这个mask是在self-attention中实现的),然后向右平移一个位置,从而能够使得其只看到当前位置前面的元素。
Attention机制
attention机制中,有query、key和value(都是向量)。其中只有一个query,而key和value有很多,并成对存在。计算时,query和每个key进行计算,得到attention scores;attention scores作为weights将对values进行weighted sum操作,得到输出。
Scaled Dot-Product Attention
这是本研究提出的新的attention计算方式
这里设定query和key的维度是\(d_k\),value的维度是\(d_v\)。我们将所有的query、key和value都组合成matrix,分别记做\(Q,K,V\),即:
\[dim(Q)=(|Q|,d_k),\quad dim(K)=(|S|,d_k),\quad dim(V)=(|S|,d_v)\]
其中\(|Q|\)表示query的数量,\(|S|\)表示key-value pairs的数量,这一般就是序列的长度。
我们进行如下计算:
\[Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V\]
现在只关注于一个样本。
前面的softmax计算的就是attention score,得到的维度是\(|Q|\times|S|\),即对于每个query,在序列的每个位置上都有一个分数,每一行之和是1。再乘以\(V\),最终结果的维度是\(|Q|\times d_v\),即对于每个query都有一个结果。
对于attention来说,最常用的就是additive attention和dot-product attention。dot-product attention相对于additive更加有效率,因为其可以利用矩阵乘法进行加速。
如果\(d_k\)不大,则两者的效果差不多。但当\(d_k\)比较大时,additive attention要优于dot-product attention。本研究怀疑这是因为当\(d_k\)较大时计算的内积比较大,会进入softmax的梯度消失区域,所以这里使用\(\sqrt{d_k}\)进行scale。
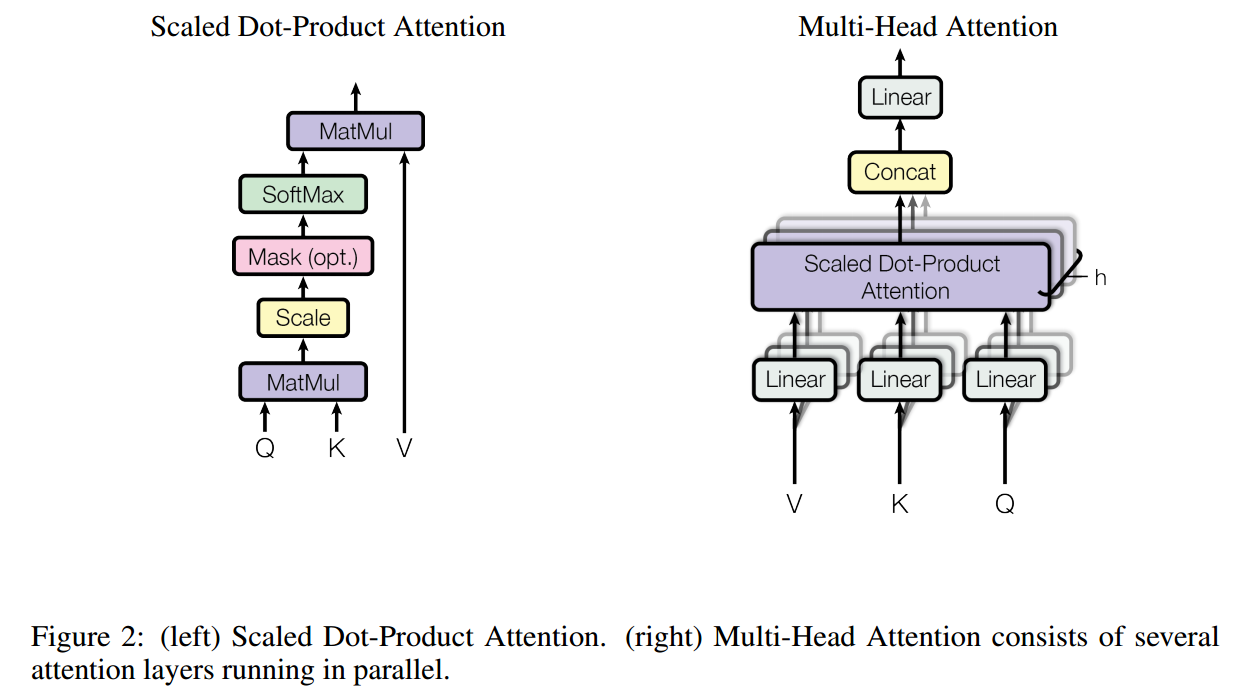
Multi-head Attention
在进行注意力机制的计算的时候,我们会先分别使用3个线性映射将\(Q,K,V\)映射到指定的\(d_k,d_k,d_v\)维度,然后再使用上面所描述的attention机制,得到\(d_v\)维度的结果。
线性映射前\(Q,K,V\)有着相同的维度\(d_{model}\)。使用不同的参数来进行映射,意味着对于\(Q,K,V\),其提取的信息应该是不同的。
multi-head attention就是平行的进行多次上面的操作,然后将结果concat到一起,最后再执行一次线性映射,得到输出:
\[ head_i = Attention(QW_i^Q,KW_i^K,VW_i^V) \\ MultiHead(Q,K,V)=Concat(head_1,\dots,head_h)W^O \]
其中\(W_i^Q\in\mathbb{R}^{d_{model}\times d_k},W_i^k\in\mathbb{R}^{d_{model}\times d_k},W_i^V\in\mathbb{R}^{d_{model}\times d_v}\)和\(W^O\in\mathbb{R}^{hd_v\times d_{model}}\)
本研究中,\(h=8\)(8个heads),\(d_k=d_v=d_{model}/h=64\),\(d_{model}=512\)。
在模型中,各处使用的attention是不一样的:
encoder-decoder attention layer(也就是decoder中插入的第二个attention layer)
它的query是来自上一个decoder layer;其keys和values是encoder的输出。这使得进行decoder的每次输出的时候,都会将整个encoder序列都看一遍。【31,2,8】
encoder使用是self-attention,其query、key和value都是前一层的输出。
decoder中的第一个sublayer也是self-attention,其接受的是输出序列。为了保证自回归假设,需要在scaled dot-product attention时进行mask(输入softmax之前,将需要去掉的值设为\(-\infty\))。
Position-wise的FC Layers
我们可以看到,attention sublayers中并没有加入多少非线性,非线性主要是由FC layers加入的。
每个位置上都使用一个权重共享的fc,实际上是使用\(1\times 1\)卷积实现的。
实际上叠加了2层fc,中间夹了一个ReLU,输入和输出自然是\(d_{model}=512\),中间层节点数是\(2048\)。
Embedding and Softmax
我们使用的数据是预先学习好的embedding,其维度是\(d_{model}\)。
同样,我们使用一个linear transformation和一个softmax来根据decoder输出的embeddding来预测是哪个词。做法类似【24】。
位置编码
整个模型中没有利用到位置信息,所以需要想办法将这个信息放到模型中。
位置编码要求将位置也编码成\(d_{model}\)维度的向量,有多种方式【8】。本研究中使用的是下面的:
\[ PE_{(pos,2i)}=sin(pos/10000^{2i/d_{model}}) \\ PE_{(pos,2i+1)}=cos(pos/10000^{2i/d_{model}}) \]
其中\(pos\)表示位置,\(i\)表示维度。
本研究也试验了学习一个位置编码,但其效果和上面这个相差无几。
自注意力
这里将self-attention和cnn、rnn进行了比较,叙述为什么使用self-attention。
这里在3个方面进行了讨论:
- 每一层的计算复杂度
- 可以并行化的计算量
- 网络中远程依赖关系的路径长度
下表是其比较结果:

结论:
除了rnn之外,其他模型的并行化都较好
如果模型的序列长度小于表示的维度,则self-attention是要比rnn计算量小的,如果想要进一步缩小self-attention的计算量,可以使用只限制在邻域上的self-attention,但其路径长度会随之增加。
cnn一般来说计算复杂度要高于rnn和self-attention。分离卷积可以有效降低计算量(\(O(knd+nd^2)\)),但相对于self-attention和point-wise fc来说依然计算量较高。
cnn另一个问题是其学习远程依赖的能力,普通的cnn的路径长度是\(O(n/r)\),就算使用空洞卷积,路径长度依然有\(O(\log_k(n))\)。
训练
数据集:
standard WMT 2014 English-German dataset,包含4.5m个sentence pairs。sentences使用byte-pair encoding【3】,37000个tokens。
larger WMT 2014 English-French dataset,包含36m个sentences,32000个tokens。
硬件:
8个NVIDIA P100 GPUs,每个training step是0.4s。
train base models 100000 steps(12h);train big models,每个step是1.0s,300000 steps(3.5d)。
Optimizer:
Adam(\(\beta_1=0.9,\beta_2=0.98,\epsilon=10^{-9}\))
学习率使用下面的公式进行改动:
\[lr=d_{model}^{-0.5}\cdot min(step_num^{-0.5},step_num\cdot warmup_steps^{-1.5})\]
正则化,使用3种:
- 每个sub-layer的输出都进行一次dropout,然后才和输入相加进行layer norm,\(P_{drop}=0.1\)。
- embeddings和positional encodings相加后,进行一次dropout,\(P_{drop}=0.1\)。
- 使用label smoothing \(\epsilon_{ls}=0.1\)【30】。
Results
机器翻译
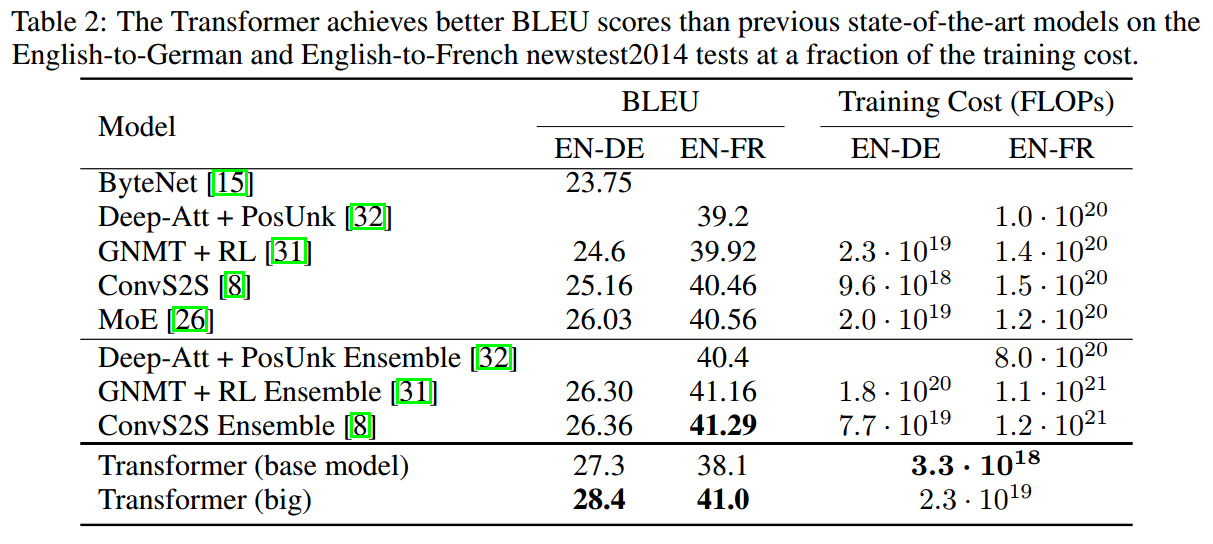
base model的预测结果是最后5个checkpoints的结果。big model是最后20个checkpoints的结果。
base model和big model的配置在下面。
模型变体
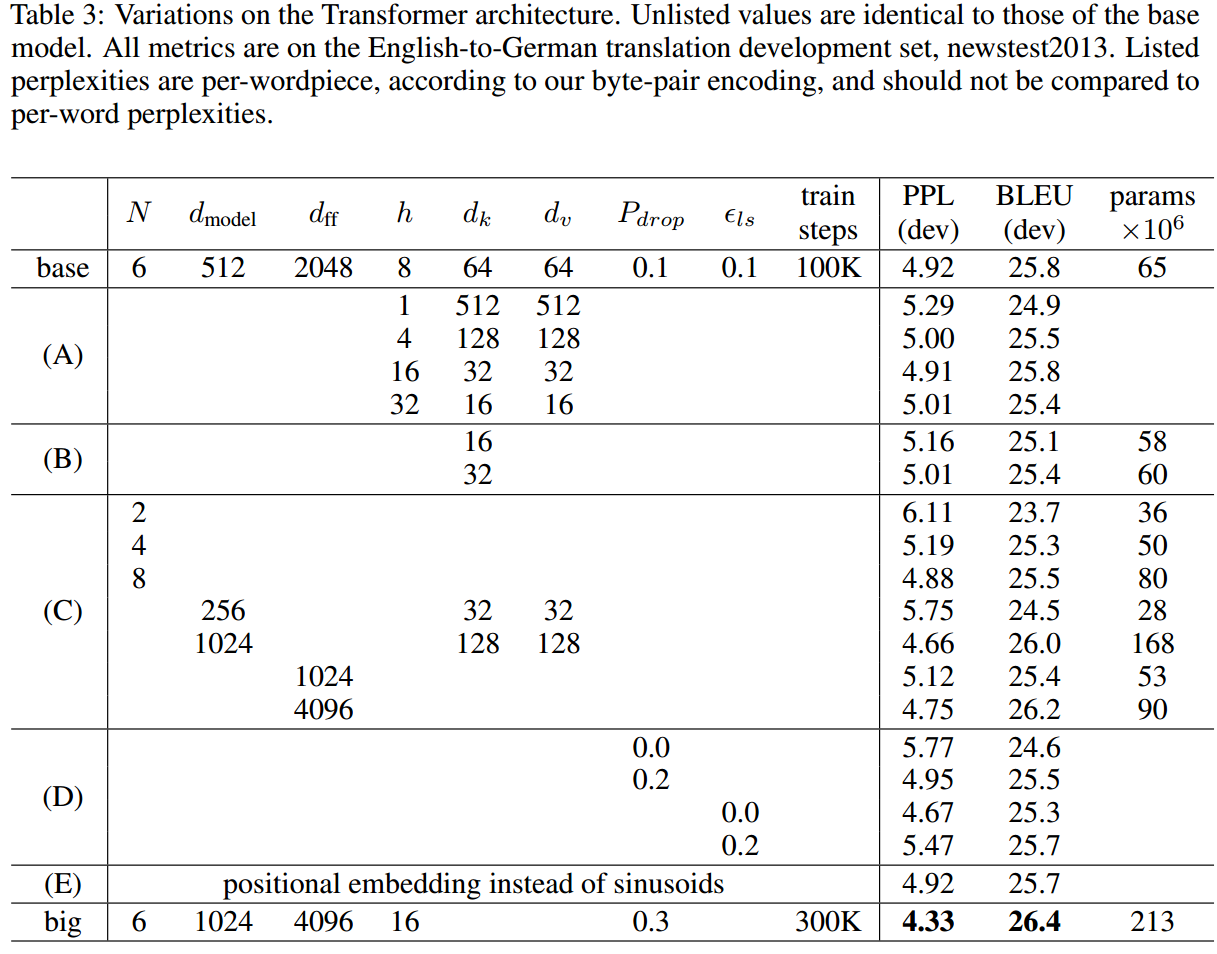
这里改变模型的不同超参数,然后去探索不同参数的影响。结果在tab3中。
Conclusion
未来的一个研究方向可能是研究local restricted attention(只关注于neighborhoods),从而提高其对于大型输入、输出的处理能力。
Questions
关于实现:
- pytorch有直接的实现
- 对于pointwise fc,在pytorch中没有必要使用1x1 cnn来实现,linear也有此功能。



