NICE: NON-LINEAR INDEPENDENT COMPONENTS ESTIMATION
- 杂志: ICLR 2015
- IF: None
- 分区: None
Introduction
深度学习实际上是一个表示学习,自然带出一个问题:
什么是好的表示?
基于最近的研究【Kingma and Welling, 2014; Rezende et al., 2014; Ozair and Bengio, 2014】,本研究认为:
一个好的表示意味着数据的分布容易被建模。
本研究希望能够学习一个transformation(随机变量函数)\(h=f(x)\),可以将数据映射到新的空间,而在新的空间中各成分是独立的:
\[p_H(h)=\prod_{d}{p_{H_d}(h_d)}\]
如果\(f\)是可逆的(invertible)并且输入维度和输入维度相同,则可以得到:
\[p_X(x)=p_H(f(x))|\det \frac{\partial f(x)}{\partial x}|\tag{1}\]
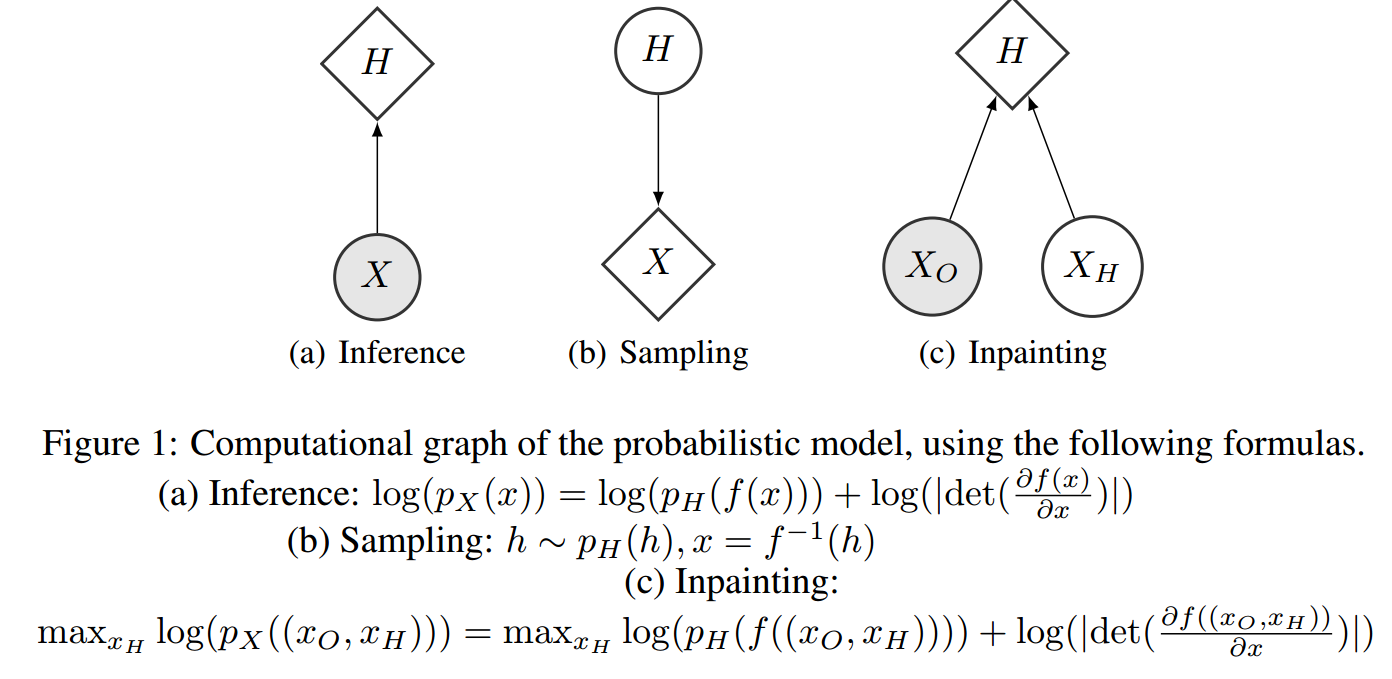
根据此公式我们可以计算给定\(x\)的概率密度(Inference)。
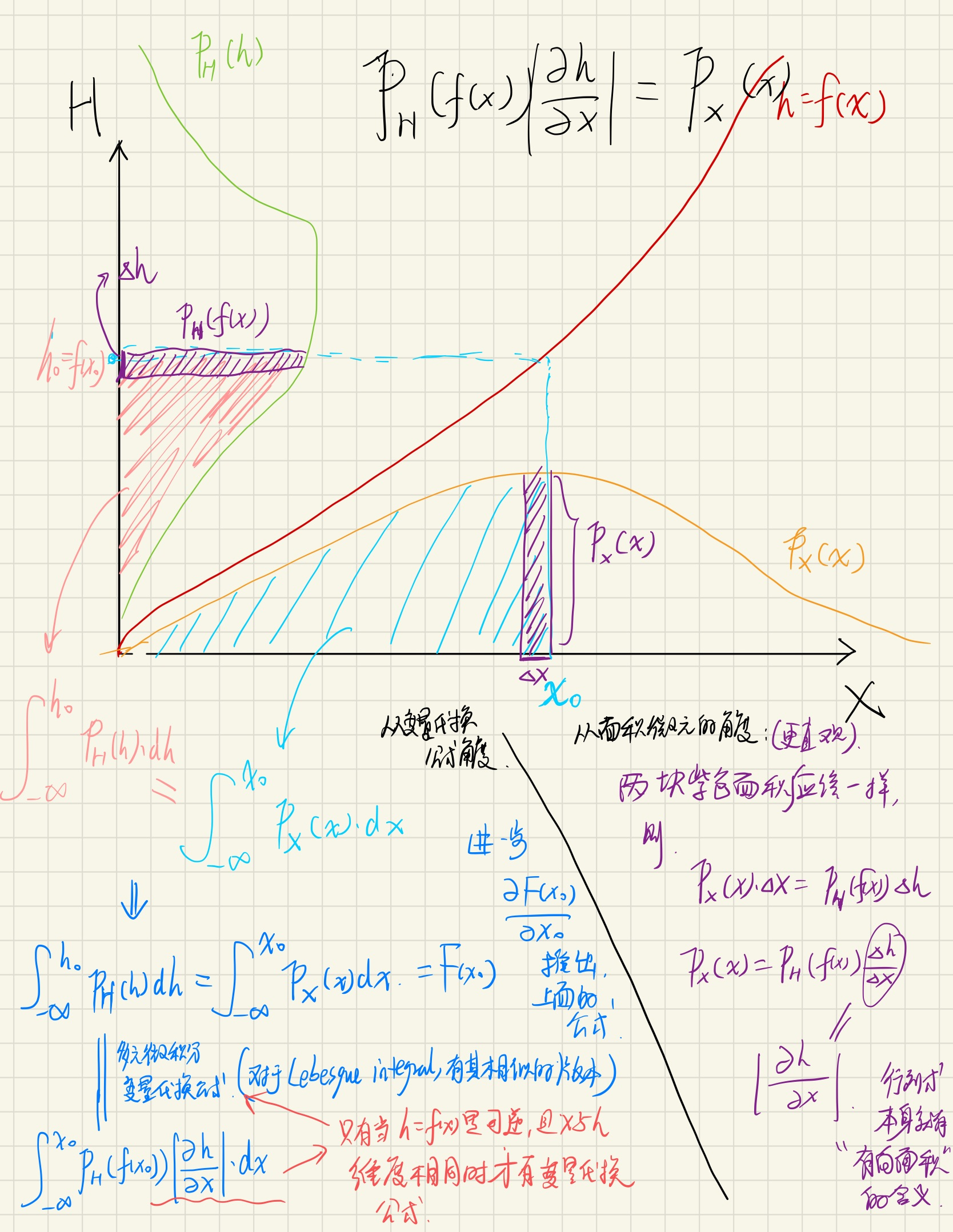
如果\(f\)的逆映射我们可以得到,则对\(X\)进行采样(sample),就可以以下面的形式进行:
\[h\sim p_H(h),\quad x=f^{-1}(h)\tag{2}\]
而我们进行训练可以以下面的方式,应用极大似然法(learning):
\[\max_{f}{\log(p_X(x))}=\max_{f}\{\log(p_H(f(x)))+\log(|\det(\frac{\partial f(x)}{\partial x})|)\}\tag{3}\]
本研究的贡献在于,经过特殊的设计,可以通过NN来拟合\(f\),并且其计算雅克比行列式和\(f^{-1}\)非常方便。
相关研究
DBM【Salakhutdinov and Hinton, 2009】,需要使用MCMC采样,而且无法获得明确的log-likelihood的估计。就算是使用已知最好的技术——annealed importance sampling(AIS)【Salakhutdinov and Murray, 2008】也会过度乐观【Grosse et al., 2013】。
至于有向图模型,VAE【Kingma and Welling, 2014; Rezende et al., 2014; Mnih and Gregor, 2014; Gregor et al., 2014】得到了极大的发展。
但VAE使用的是log-likelihood的变分下界,其得到的可能是一个次优解,使得生成的结果带有更多的噪声,看起来不太自然。
实际上,NICE可以看做是一类特殊的VAE。其中的encoder是\(f\),decoder是\(f^{-1}\),其KL散度项就是\(\log(p_H(f(x)))\),其entropy项就是\(\log(|\det\frac{\partial f(x)}{\partial x}|)\),反应的是在每一点上局部概率的“膨胀比例”。
ICA【Hyvarinen and Oja, 2000】
【Rippel and Adams, 2013】提出了学习这些transformations的想法,但因为没有使用双射,所以被迫使用一个带有regularization的AEs来解决的。
GAN
triangular structure在另外一类density models也出现过——neural autoregressive networks【Bengio and Bengio, 2000】,其最近的成功是NADE【Larochelle and Murray, 2011】。
但作为一个自回归模型,其在采样的时候是无法并行化的,从而使得其在高维数据上应用有限。
Methods
学习
这里对learning的过程再进行一下解释。
分布\(p_H(h)\)这里称为prior distribution,如果其实factorial(各个维度是独立的),则此时公式3的估计称为non-linear independent components estimation(NICE)。
\[\max_{f}{\log(p_X(x))}=\max_{f}\{\sum_{d=1}^D\log(p_{H_d}(f_d(x)))+\log(|\det(\frac{\partial f(x)}{\partial x})|)\}\tag{4}\]
我们将后面的Jacobian determinant部分看做是一个正则化项,则作用是:使得函数\(f\)在数据点出现的位置有更高的密度增长,因为\(p_H(h)\)是预先固定的,则\(f\)变化将把数据点都推到有更高概率密度的地方。
架构
这里将\(f\)称为encoder、将\(f^{-1}\)称为decoder。
我们先聚焦于单个layer的计算,此时我们的目标有两个:构造一个双射函数、其Jacobian determinant好算。
这两者也是相关的,如果我们构造的Jacobian matrix是可逆的,则函数也就是双射的。
仿射变换
最早的想法是layer是一个affine transformation(线性的,就是乘以一个矩阵\(W\))。
这样一个affine transformation的Jacobian matrix就是\(W^T\),为了让这个矩阵的行列式好算,可以让这个\(W\)是对角、上三角、下三角矩阵。
当我们堆叠多层的时候,上三角、下三角矩阵的相乘也能够覆盖一部分普通的square matrix。
但总的来说,这种方法能够拟合的函数只是线性的,而且也只是线性函数的一部分。
现在我们进一步推广上面的想法,我们现在去考虑这样一组函数,其Jacobian是上三角或下三角即可。
耦合层
\(x\in\mathcal{X}\),\(I_1\)和\(I_2\)是index \([1,D]\)的一个划分,其中\(d=|I_1|,\)\(m\)是定义在\(\mathbb{R}^{d}\)上的一个任意函数。现在我们定义\(y=(y_{I_1},y_{I_2})\):
\[ y_{I_1} = x_{I_1} \\ y_{I_2} = g(x_{I_2};m(x_{I_1})) \]
其中\(g:\mathbb{R}^{D-d}\times m(\mathbb{R}^d)\to\mathbb{R}^{D-d}\)称为general coupling law,给定第二个参数(\(m(x_{I_1})\))后,这个函数是对于第一个参数(\(x_{I_2}\))可逆的。
我们可以计算这个函数的Jacobian matrix:
\[ \frac{\partial y}{\partial x} = \begin{bmatrix} I_d & 0 \\ \frac{\partial y_{I_2}}{\partial x_{I_1}} & \frac{\partial y_{I_2}}{\partial x_{I_2}} \end{bmatrix} \]
其中\(I_d\)是\(d\)维的单位矩阵。我们发现,\(\det \frac{\partial y}{\partial x}=\det\frac{\partial y_{I_2}}{\partial x_{I_2}}\)。
另外,也容易验证,该映射\(y=f(x)\)是可逆的,其逆映射是:
\[ x_{I_1}=y_{I_1} \\ x_{I_2}=g^{-1}(y_{I_2};m(y_{I_1})) \]
我们称呼这是一个带有coupling function \(m\)的coupling layer。
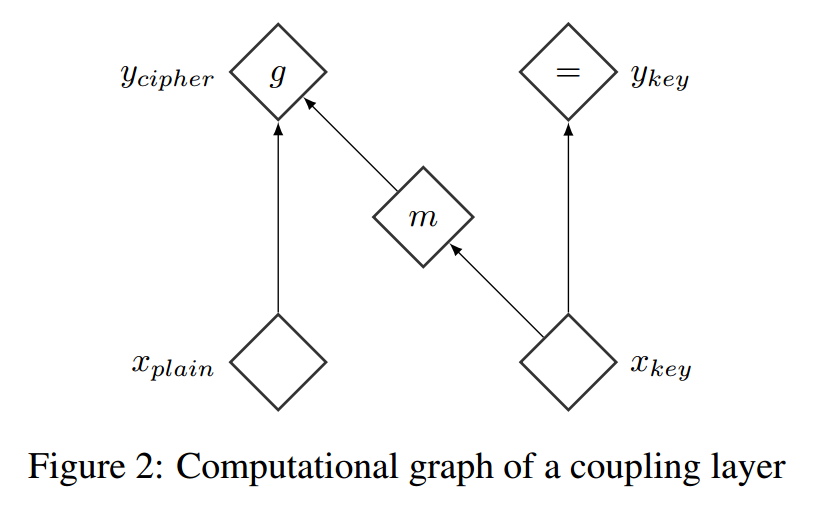
加性耦合层
为了简单,我们直接使用additive coupling law \(g(a;b)=a+b\),则这时候我们得到了最常见到的形式:
encoder:
\[ y_{I_1} = x_{I_1} \\ y_{I_2} = x_{I_2}+m(x_{I_1}) \]
decoder:
\[ x_{I_1}=y_{I_1} \\ x_{I_2}=y_{I_2}-m(y_{I_1}) \]
逆映射和正映射的计算量是相同的。
另外,其Jacobian determinant是1。
这时,我们可以令\(m\)是一个从\(d\)维向量映射到\(D-d\)维向量的NN。
其实,还有其他很多coupling law可以选择,比如:
multiplicative coupling law :
\[g(a;b)=a\odot b\]
affine coupling law:
\[g(a;b)=a\odot b_1+b_2\]
当然,additive coupling因为其简单,稳定性更好。
结合多个coupling layers
因为有一部分维度的数据是不变的,所以我们需要组合多个coupling layers、并且在不同layers间划分的两部分数据所扮演的角色。至少需要3层coupling layers,一般来说要用4层。
组合之后,整个网络的Jacobian determinant也是1,也就是说保持体积的。但注意到,尽管我们使用的数据有\(D\)维,但很多维度可能是冗余的,所以在我们进行encoder的时候也保持这个维度,会浪费很多维度,使得效果不好。
解决方法是每个维度再乘以一个可训练的缩放系数\(h=s\cdot f(x)\),这样整个映射依然是可逆的,但模型可以自动进行维度的“缩放”,如果\(h\)的某个维度不重要,则该维度的缩放系数会趋于无穷大,使该维度失效。
此时,我们的极大似然估计也需要进行一定的改变:
\[\max_{f}{\log(p_X(x))}=\max_{f}\{\sum_{d=1}^D[\log(p_{H_d}(s_df_d(x)))+\log(s_d)]\}\tag{5}\]
尺度变化参数的另一个理解:
如果我们使用的prior distribution是独立的标准正态分布,则其方差都为1。但我们也可以让其方差不为1,而是一个可训练的参数。此时这个可训练的方差参数和上面的尺度参数是一个东西(尺度参数是方差参数的倒数)。
当尺度参数趋于无穷大的时候,方差趋于0,此时该维度的正态分布坍缩为一个单点,也就意味着减小了一个维度。就算不使该维度坍缩,但仅仅是降低其方差也意味着该维度信息量的降低。
先验分布
介绍了2种先验分布:
- gaussian distribution
- logistic distribution
本研究使用的是logistic distribution,其拥有更好的梯度特性。
Results
使用的数据集:
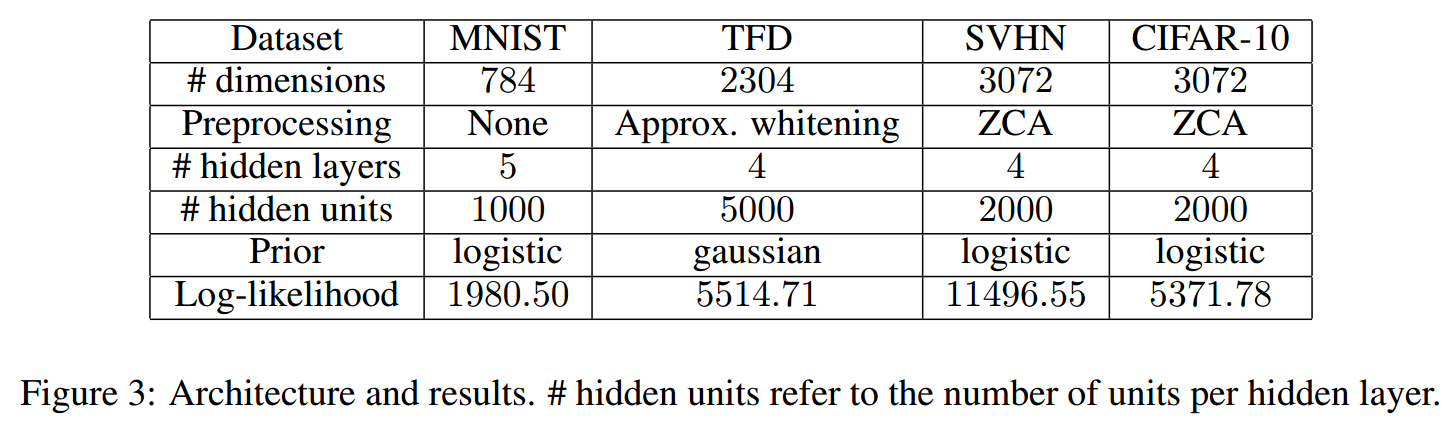
首先需要对其进行连续化(加上一个1/256均匀分布的噪声,然后将数据归一化到0——1,对于CIFAR-10是1/128和-1——1)
网络架构:
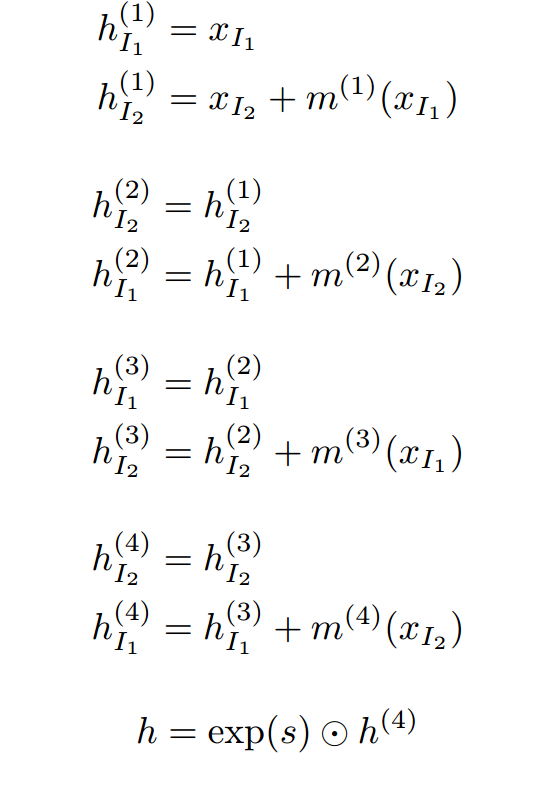
其中\(I_1\)是奇数,\(I_2\)是偶数。\(m\)是5层的nn,其中最后一层不加ReLU激活。对于MNIST,hidden units是1000,对于TFD是5000,对于SVHN和CIFAR-10是2000。
prior distribution是logistic distribution。
训练使用的是Adam,lr=\(10^{-3}\),momentum是0.9,\(\beta_2=0.01,\lambda=1,\epsilon=10^{-4}\)。1500个epochs后在valid data上通过log-likelihood选择最好的model。
结果如下:
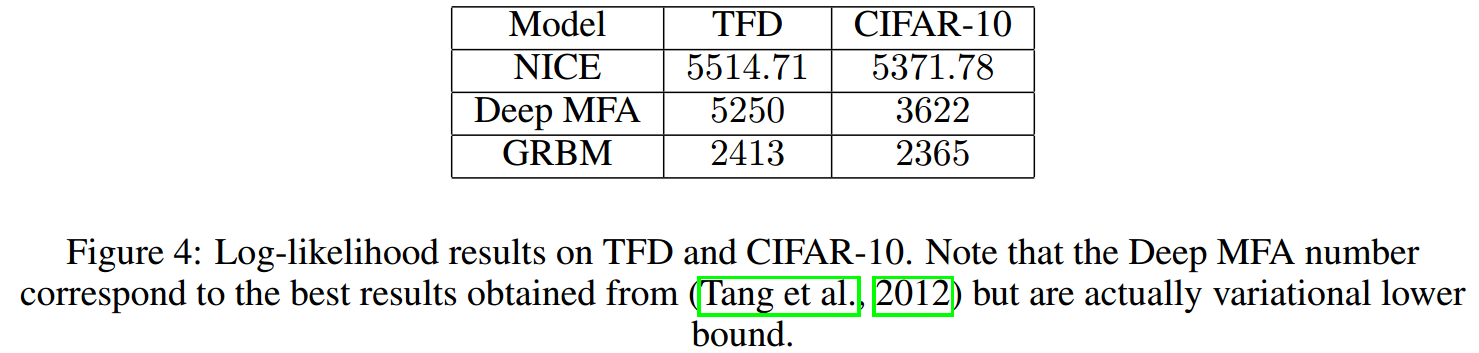
下面是NICE的采样:

Inpainting任务
这里使用一个训练好的模型,然后进行projected gradient ascent,其方式如下:
观察到的数据是\(x_O\);
使用下面的公式进行迭代:
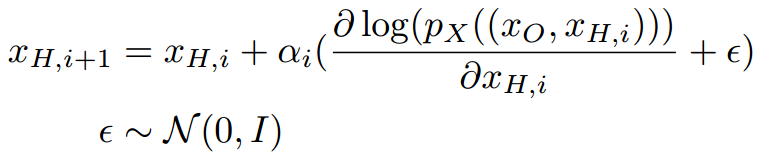
将最后得到的\(x_H\)使用模型映射回\(x\),得到填补好的图片。
下面是结果:

Conclusion
- 当前模型的架构似乎可以整合更多归纳信息,比如toroidal subspace analysis(TSA)【Cohen and Welling, 2014】。



