Variational Graph Convolutional Networks
- 杂志: None
- IF: None
- 分区: None
Introduction
GCN解决了节点的半监督分类问题,并且结构简单,不需要进行特征分解;
但其一个主要假设是使用的graph是正确可靠的(这也是大多数GNNs的假设),但实际上并不是(噪声影响、和分类问题相关程度不高等);
本研究试图通过bayesian方法来的图的结构进行优化,并克服了以下两个问题:
使用随机变分推断去计算后验分布;
需要优化\(O(N^2)\)个参数;
相关工作
- 【28】第一次试图对GNN进行概率描述,其将graph视为一个mixed membership stochastic block models【1】,但这样的方法并没有将参数视为后验的(即随观测发生变化);
- 【20】使用到了高斯过程(GP)进行建模啊;
- 【5】去开发了一种生成模型来进行图结构的学习;
- 【14】提出了变分图自编码器,其和本文的工作目的并不一致。
Methods
Bayesian GCNs
这里介绍likelihood和prior
\(\mathbf{X}\in\mathbb{R}^{N\times D}\)是\(N\)个实例的\(D\)维features,其对应的labels是\(\mathbf{Y}=\{\mathbf{y}_n\}\)。这些labels有些是观测到的,而另外一些是未观测到的,其都是one-hot向量:\(\mathbf{y}_n\in\{0,1\}^C\)。我们的任务是使用上面的数据对未观测的标签进行预测,这里基于的框架是GCN。
\(\mathcal{G}=(\mathcal{V},\mathcal{E})\)表示一个无向图,其中有\(N\)个节点:\(v_i\in\mathcal{V}\),其对应的边是\((v_i,v_j)\in\mathcal{E}\),邻接矩阵是binary的:\(\mathbf{A}\in\{0,1\}^{N\times N}\)。
依据上面的设置并假设可观测的labels是条件独立的,则我们可以写出:
likelihood
\[ p_{\mathbf{\theta}}(\mathbf{Y}^o|\mathbf{X},\mathbf{A}) = \prod_{\mathbf{y}\in\mathbf{Y}^o}{p_{\mathbf{\theta}}(\mathbf{y}_n|\mathbf{X}, \mathbf{A})}\quad\text{with}\quad p_{\mathbf{\theta}}(\mathbf{y}_n|\mathbf{X}, \mathbf{A})=Cat(\mathbf{y}_n|\mathbf{\pi}_n) \]
如果是使用GCN的话,我们有:
\[\mathbf{\Pi}= \mathbf{f}^{L}(\mathbf{X},\mathbf{A})= softmax(\tilde{\mathbf{D}}^{-1/2}\tilde{\mathbf{A}}\tilde{\mathbf{D}}^{-1/2} relu(\tilde{\mathbf{D}}^{-1/2}\tilde{\mathbf{A}}\tilde{\mathbf{D}}^{-1/2}\mathbf{W_0})\mathbf{W_1} )\]
其中\(\mathbf{\Pi}\)的每一行是一个\(\mathbf{\pi}_n\)。
接下来,我们考虑:
graph priors
\[p(\mathbf{A})=\prod_{ij}p(A_{ij})\quad\text{with}\quad p(A_{ij})=Bern(A_{ij}|\rho_{ij}^o)\]
注意到,这个先验是可以通过多种方式来构造的,比如我们已知一个图结构,则我们可以通过下面的方式来构造这个先验:
\[\rho_{ij}^o=\bar{\rho}_1\bar{\mathbf{A}}_{ij}+\bar{\rho}_0(1-\bar{\mathbf{A}}_{ij})\]
其中\(\bar{\mathbf{A}}\)是我们手上拥有的图邻接矩阵(binary),\(0\lt\bar{\rho}_1,\bar{\rho}_0\lt1\)是超参数。
即这里的先验并不是说graph有边的地方就是1、无边的地方就是0,而是有边的地方是\(\bar{\rho}_1\)、无边的地方是\(\bar{\rho}_0\)。
依靠平滑参数进行graph structure inference
这里介绍如何通过likelihood和prior来推断posterior
这里的关键在于对后验的structure进行估计:\(p(\mathbf{A}|\mathbf{X},\mathbf{Y}^o)\propto p_{\mathbf{\theta}}(\mathbf{Y}^o|\mathbf{X},\mathbf{A})p(\mathbf{A})\),这里我们使用VI【11】的方法来对其进行估计。
变分分布
假设graph中每条边存在与否服从的伯努利分布是独立的,则后验分布的变分分布有如下的形式:
\[q_{\mathbf{\phi}}(\mathbf{A})=\prod_{ij}q(A_{ij})\quad\text{with}\quad q_{\mathbf{\phi}}(A_{ij})=Bern(A_{ij}|\rho_{ij})\]
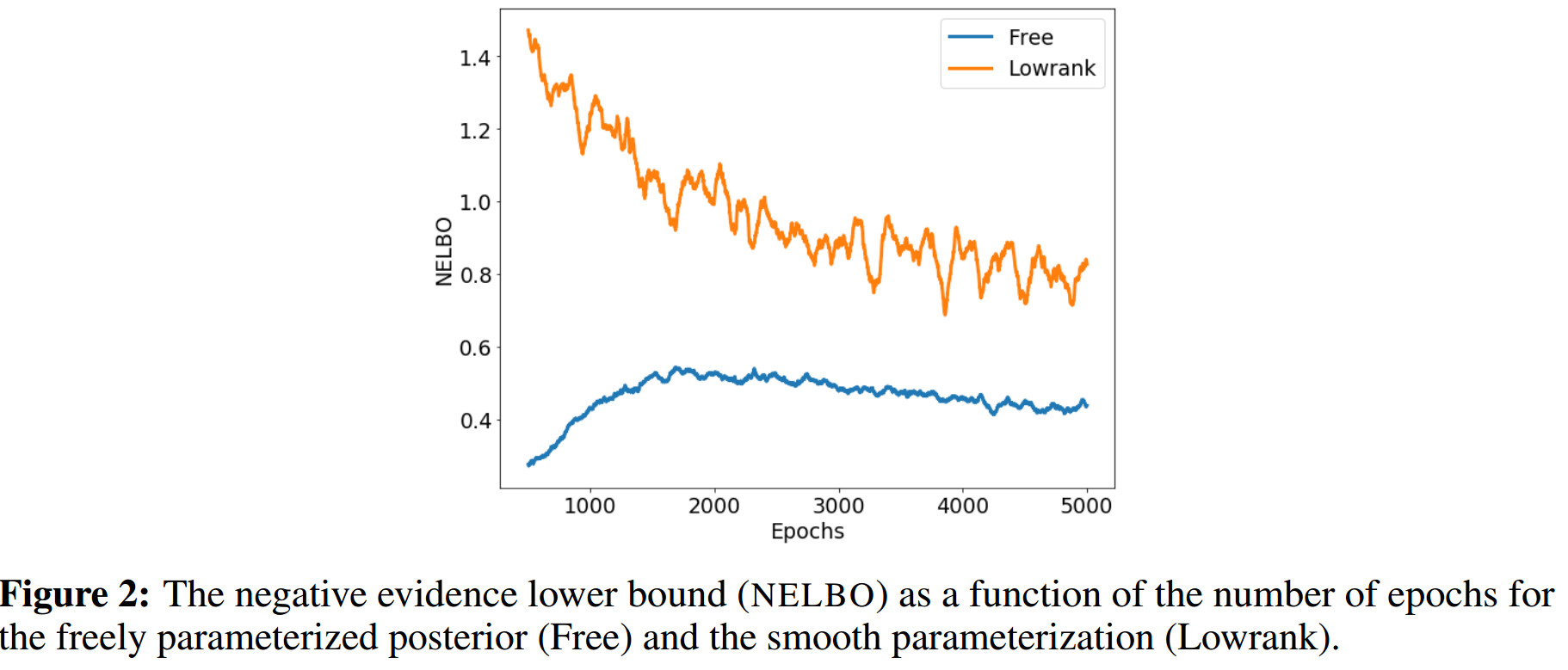
\(\mathbf{\phi}\)表示的是变分分布的可训练参数,在上面的形式中,可以看到,这个参数就是\(\mathbf{\phi}={\rho_{ij}}\),这称为“free” parameterization。
如果我们有1000个nodes,则我们设置的参数的数量是1000000,也就是说free parameterization带来的是参数数量的过多。
实际上条件独立性是一个非常强的假设,这也是不符合实际的,这也是导致参数数量过多的一个原因。大量的参数\(\rho_{ij}\)实际上是高度相关的,比如说参数\(a_1\)和\(a_2\)高度相关,则当我们进行梯度下降进行训练的时候,更新\(a_1\)或\(a_2\)都会得到相似的结果,这反而平摊了整个效应,或者导致梯度的剧烈震荡和不稳定。
在supplementary中,fig2也证明了以上的观点。
相对的,有以下的设置方法,称为"smooth" parameterization:
\[\rho_{ij}=\sigma(\mathbf{z}_i^T\mathbf{z}_j+b_i+b_j+s),\quad \mathbf{z}_i\in\mathbb{R}^d,\quad \{b_i,s\in\mathbb{R}\}\quad i,j=1,\dots,N \]
我们可以看到,实际上,这里就是尽量使用较少的参数来生成\(\rho_{ij}\)。如果将上面的式子写成矩阵形式,即: \[\Rho=\sigma(\mathbf{Z}^T\mathbf{Z}+B\mathbf{1}^T+\mathbf{1}B^T+s)\] 其中\(\mathbf{Z}=(\mathbf{z}_1,\dots,\mathbf{z}_N)^T\),\(B=(b_1,\dots,b_N)^T\),\(\mathbf{1}=(1,\dots,1)^T\)。 其实就是使用低秩矩阵,并且通过dot-product来构造这个低秩矩阵,使得参数之间存在相关。
现在,我们开始来最小化ELBO来得到\(\mathbf{\phi}\)的估计,其中最general的方法是score function method【22】,其使用Monte Carlo方法得到了梯度的无偏估计,但方差太大【23】。
另外一条路,则是使用re-parameterization trick【13,24】,其会极大地降低估计的方差。但不幸的是,这无法应用到离散分布中。所以我们采用【10,16】的Concrete distributions:
\[q_{\phi}(\mathbf{A}_{ij})=BinConcrete(\mathbf{A}_{ij}|\rho_{ij},\tau)\]
gambel-softmax采样【10】的改进。
这里我们对BinConcrete的形式进行一定的介绍,详细请见其原文【16】:
\[A_{ij}\sim BinConcrete(\lambda_{ij},\tau)\quad\Leftrightarrow\quad A_{ij}=\sigma(B_{ij}),B_{ij}\sim Logistic(\frac{\log\lambda_{ij}}{\tau}, \frac{1}{\tau}) \]
\[B_{ij}\sim Logistic(\frac{\log\lambda_{ij}}{\tau}, \frac{1}{\tau}) \quad\Leftrightarrow\quad B_{ij}=\frac{\log\lambda_{ij}+L}{\tau},L\sim Logistic(0,1)\]
\[L\sim Logistic(0,1)\quad\Leftrightarrow\quad L=\sigma^{-1}(U)=\log U-\log(1-U),U\sim Uniform(0,1)\]
综合上面的式子,我们得到:
\[A_{ij}\sim BinConcrete(\lambda_{ij},\tau)\quad\Leftrightarrow\quad A_{ij}=\sigma(\frac{\log\lambda_{ij}+\sigma^{-1}(U)}{\tau}), U\sim Uniform(0,1) \]
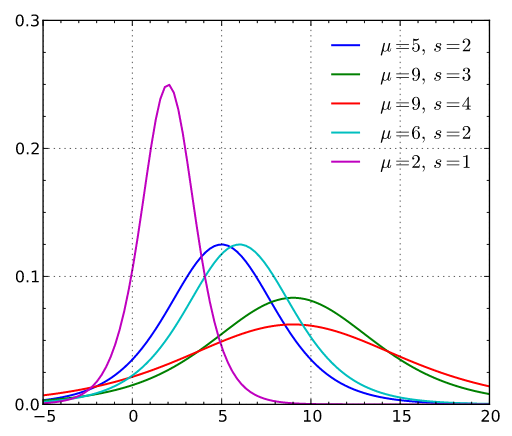
这里对Logistic分布进行一些简单的介绍,便于理解:
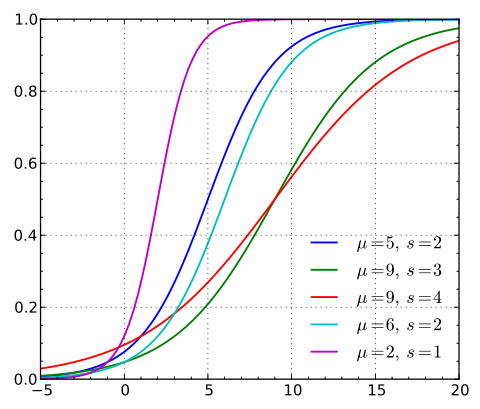
Logistic分布的累积分布函数就是logistic函数的变体,其导函数就是其密度函数,呈现中间高两头低的效果,类似正态分布。
\[F_{\mu,\sigma}(x)=\frac{1}{1+e^{-\frac{x-\mu}{\sigma}}}\] \[f_{\mu,\sigma}(x)=\frac{1}{\sigma}e^{-\frac{x-\mu}{\sigma}}[1+\exp\{-\frac{x-\mu}{\sigma}\}]^{-2}\]
其类似正态分布,也是location-scale决定了其所有性质。当\(\mu=0,\sigma=1\)时,得到的是标准logistic分布,
\[F(x)=\frac{1}{1+e^{-x}}\] \[f(x)=e^{-x}[1+e^{-x}]^{-2}\]
其图像如下:
根据“逆分布函数采样法”,我们只要找到\(F(x)\)的反函数,我们就可以进行采样,而其反函数是非常好计算的:
\[F^{-1}(x)=\log x-\log(1-x)\]
ELBO
\[\mathcal{L}_{ELBO}(\mathbf{\phi}) =\mathbb{E}_{q_{\phi}}{\log p_{\mathbf{\theta}}(\mathbf{Y}^o|\mathbf{X},\mathbf{A})} -KL[q_{\phi}(\mathbf{A})||p(\mathbf{A})]\]
其中\(p(\mathbf{A})\)是prior。
进一步,我们将不同分布的的KL散度的具体计算:
对于两个binary discrete distributions \(q(a|\rho)\)和\(p(a|\rho^o)\):
\[KL[q(a|\rho)||p(a|\rho^o)]=\rho[\log\rho-\log\rho^o] +(1-\rho)[\log(1-\rho)-\log(1-\rho^o)]\]
根据上面的式子,我们可以写出ELBO的re-parameterized version:
\[\begin{aligned} \mathcal{L}_{ELBO}(\phi)&= \mathbb{E}_{q_{\phi,\tau}(\mathbf{A})}[ \log p_{\mathbf{\theta}}(\mathbf{Y}|\mathbf{X},\mathbf{A})- \log\frac{q_{\phi,\tau}(\mathbf{A})}{p_{\tau_o}(\mathbf{A})}] \\ &=\mathbb{E}_{g_{\phi,\tau}(\mathbf{B})}[ \log p_{\mathbf{\theta}}(\mathbf{Y}|\mathbf{X},\sigma(\mathbf{B}))- \log\frac{q_{\phi,\tau}(\sigma(\mathbf{B}))} {p_{\tau_o}(\sigma(\mathbf{B}))} ] \\ &=\mathbb{E}_{g_{\phi,\tau}(\mathbf{B})}[ \log p_{\mathbf{\theta}}(\mathbf{Y}|\mathbf{X},\sigma(\mathbf{B}))- \log\frac{q_{\phi,\tau}(\sigma(\mathbf{B}))} {f_{\tau_o}(\mathbf{B})} ] \end{aligned}\]
其中 \[ g_{\phi,\tau}(\mathbf{B})=Logistic(B_{ij}|\frac{\log\lambda_{ij}}{\tau},\frac{1}{\tau}),\quad f_{\tau_o}(B_{ij})=Logistic(B_{ij}|\frac{\log\lambda_{ij}^o}{\tau_o}, \frac{1}{\tau_o}) \]
predict
预测时,使用下面的式子:
\[p(\mathbf{Y}^{u}|\mathbf{Y}^o,\mathbf{X})= \sum_{\mathbf{A}}{ p_{\mathbf{\theta}}(\mathbf{Y}^{u}|\mathbf{X},\mathbf{A}) p(\mathbf{A}|\mathbf{Y}^o,\mathbf{X})\approx \frac{1}{S}\sum_{s=1}^S{ p_{\mathbf{\theta}}(\mathbf{Y}^u|\mathbf{X},\mathbf{A}^{(s)}) } }\]
其中\(\mathbf{A}^{(s)}\)是从后验分布\(q_{\phi}(\mathbf{A})\)中的采样,而\(p_{\theta}(\mathbf{Y}^u|\mathbf{X},\mathbf{A})\)是通过GCN得到的likelihood。
Results
数据集

- citation network的节点是文档,边表示两篇文章之间是否引用,节点类别是文章的subject。
- TWITTER的节点是Twitter user,边表示用户转换过另外一个用户的推文,每个节点的特征是用户的行为和用户的tweet texts,节点的类别是用户的hatefulness status。
我们corrupt网络,通过增加一些fake links,增加的fake links的数量与存在的边的数量的比例是固定的,这个参数称为corruption factor。
实现细节
对于先验分布的smoothing parameters,这里探索了多个:\(\bar{\rho}_1=\{0.25,0.5,0.75\},\bar{\rho}_0=10^{-5}\)
对于standard GCN,使用的就是标准的2层GCN网络,最小化cross-entropy来进行训练,并使用了dropout、L2regularization、Glorot weight initialization和row-normalization of input-feature vectors。超参数使用【15】中效果的最好的那一组(dropout rate=0.5,L2 regularization=\(5\times10^{-4}\),16 hidden units)。使用Adam optimizer(lr=0.01)。
GAT,使用是【26】中的架构:第一层K=8,隐层变量的维度F=8,激活函数是ELU,第二层直接进行分类。L2=0.0005,dropout=0.6。
GraphSAGE,使用mean aggregator functions,邻接点采样深度K=2,邻接点数量S1=S2=32,dropout=0.5、L2=0.0005。
对于本研究的方法,GCN使用的设置与上面的相同。对于先验分布的smoothing parameters,这里探索了多个:\(\bar{\rho}_1=\{0.25,0.5,0.75\},\bar{\rho}_0=10^{-5}\)。\(\mathbf{Z}\)的维度是\(N\times1000\),\(b_i\)和\(s\)被初始化为\(0\)和\(-20\),temperatures被设置为\(\tau_0=\tau_1=0.1\)。训练的epoches数是5000,进行梯度估计时的采样数是\(S=3\)。
结果
比较的指标是test上的acc和mean log likelihood,两个指标都是越高越好。
CITESEER和CORA的结果如下:
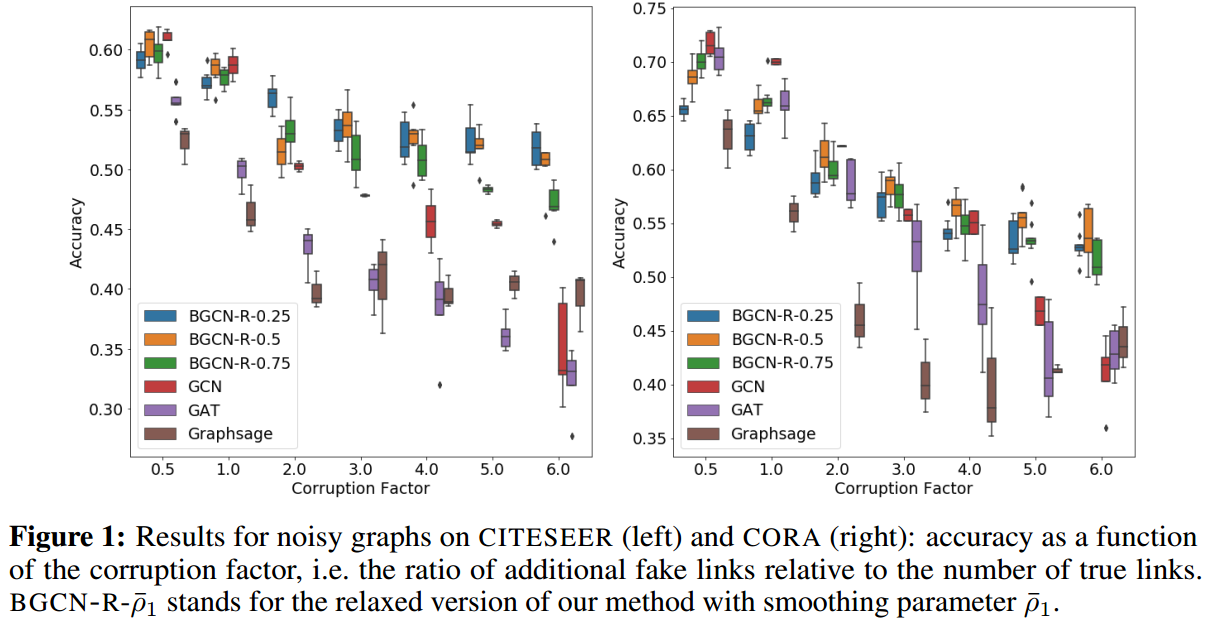
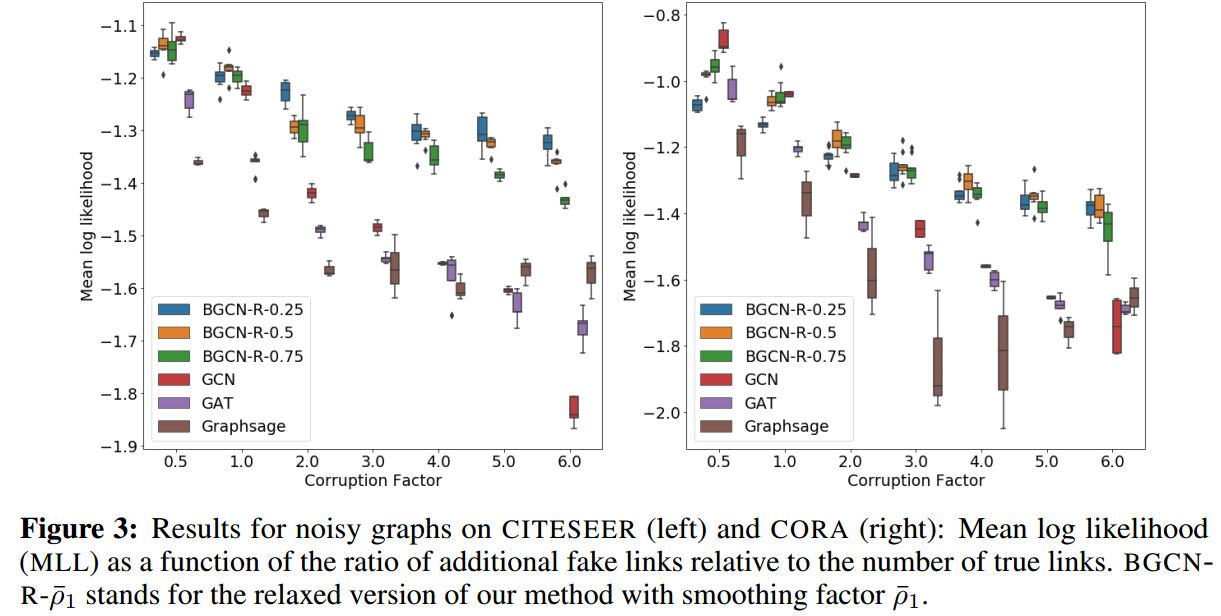
可以看到,当有较高噪声干扰的时候,该方法的效果是显著的。
进一步,本研究探索了hidden units数量(Q)和构建图时使用的邻居数(K)对性能带来的影响,这里横坐标是Q-K:
这里构建网络的方法参照【9】,即使用一个单隐层的NN(隐层节点数为16或32),带有dropout=0.5,然后我们将隐层节点取出,利用其构建一个graph。
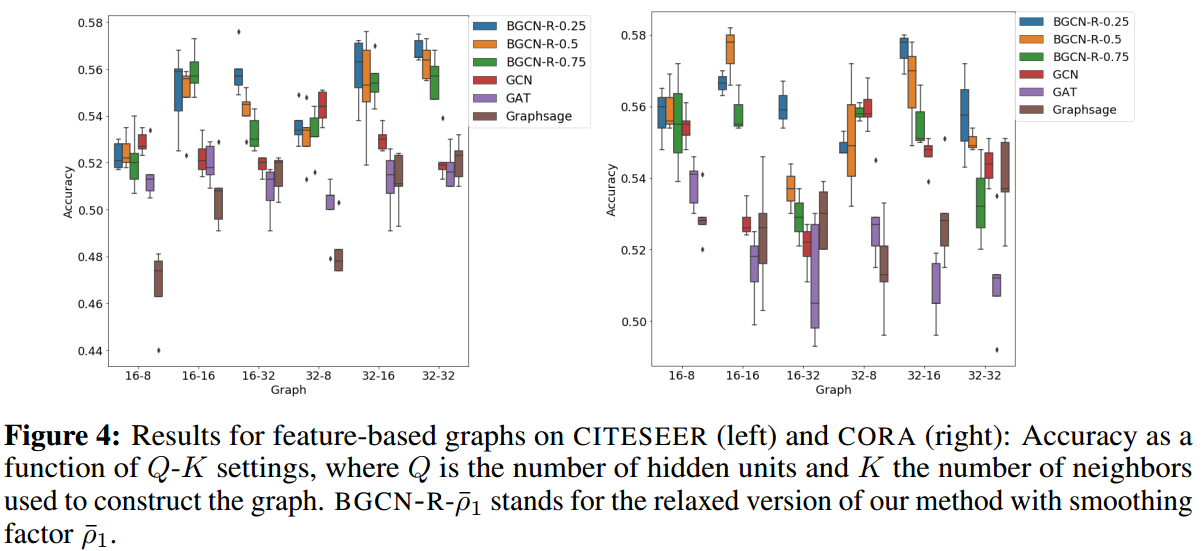
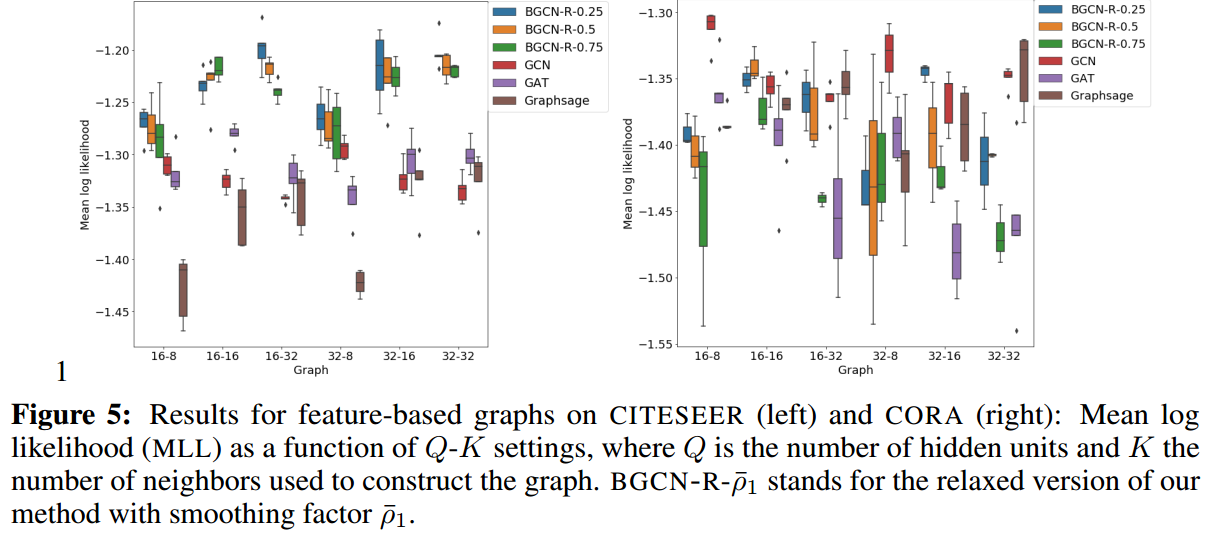
至于TWITTER数据的结果: