Variational Graph Auto-Encoders
- 杂志: None
- IF: None
- 分区: None
Introduction
本研究提出了一种新的graph上的无监督学习架构,称为variational graph autoencoder(VGAE),其基于VAE,来学习可解释的latent representation。这里我们使用GCN作为encoder、inner product作为decoder,并应用到citation networks上的link prediction任务,并取得了不错的效果。
Methods
这里使用的是undirected、unweighted graph \(\mathcal{G}=(\mathcal{V}, \mathcal{E})\),其中节点数为\(N=|\mathcal{V}|\),graph的邻接矩阵为\(\mathbf{A}\)、degree矩阵为\(\mathcal{D}\)。
latent variables是\(\mathbf{z}_i\),将所有节点组合成矩阵\(\mathbf{Z}\in\mathbb{R}^{N\times F}\)。节点特征矩阵为\(\mathbf{X}\in\mathbb{R}^{N\times D}\)。
Inferece model
编码器
\[q(\mathbf{Z}|\mathbf{X},\mathbf{A})=\prod_{i=1}^Nq(\mathbf{z}_i|\mathbf{X},\mathbf{A}),\quad\text{with}\quad q(\mathbf{z}_i|\mathbf{X},\mathbf{A})=\mathcal{N}(\mathbf{z}_i|\mathbf{\mu}_i,diag(\mathbf{\sigma}_i^2))\]
其中\(\mathbf{\mu}=GCN_{\mu}(\mathbf{X},\mathbf{A})\),\(\log\mathbf{\sigma}=GCN_{\sigma}(\mathbf{X},\mathbf{A})\)。这两个GCN都是2-layers,其共享第一层的参数。
Generative model
解码器
\[q(\mathbf{A}|\mathbf{Z})=\prod_{i=1}^N\prod_{j=1}^Np(A_{ij}|\mathbf{z}_i,\mathbf{z}_j),\quad\text{with}\quad p(A_{ij}|\mathbf{z}_i,\mathbf{z}_j)=\sigma(\mathbf{z}_i^T\mathbf{z}_j)\]
Learning
\[\mathcal{L}=\mathbb{E}_{q(\mathbf{Z}|\mathbf{X},\mathbf{A})} [\log p(\mathbf{A}|\mathbf{Z})]-KL[q(\mathbf{Z}|\mathbf{X},\mathbf{A})|| p(\mathbf{Z})]\]
其中\(p(\mathbf{Z})\)是先验分布,使用Gaussian prior。
训练的时候是使用full-batch gradient descent。对于featureless approach,\(\mathbf{X}\)被identity matrix替代。
GAE model
这是一个比较模型,即确定性的graph autoencoder。
\[\hat{\mathbf{A}}=\sigma(\mathbf{Z}\mathbf{Z}^T),\quad\text{with}\quad \mathbf{Z}=GCN(\mathbf{X},\mathbf{A})\]
Results
这里使用不同的方法来学习节点表示,然后使用下面的公式来对graph的link进行预测:
\[\sigma(\mathbf{Z}\mathbf{Z}^T)\]
使用的数据来自【1】,首先会将其中5%和10%的边作为validation和test去掉。
- 对于VGAE和GAE,其使用Adam(lr=0.01)训练了200个iterations,然后使用了32-dim的hidden layer和16-dim的latent variables。
- 对于SC,使用的embedding dimension是128。
- 对于DW,使用的是【8】的标准设置。
结果如下所示:
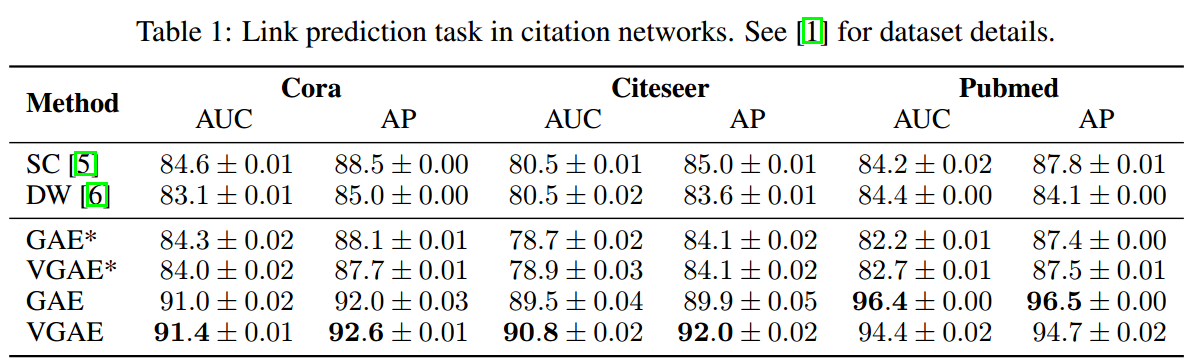
GAE和VGAE都得到了不错的结果,特别是使用上节点特征会显著提高预测结果。实际上使用Gaussian prior是个非常差的选择,但依然取得了不错的效果。
Conclusion
以后可以需要探索更合适的prior、更加灵活的generative models和随机梯度下降的使用。



