Time-to-Event Prediction with Neural Networks and Cox Regression

杂志: None
IF: None
分区: None

Introduction

本研究探索time-to-event预测的方法，其在大量的实践中有应用：
- 癌症病人的生存预测
- 客户流失
- 机械系统的失效时间
其更加注重可解释性。
在time-to-event问题中，一个重要的特点是会出现censored data。
本研究中，提出了一种将机器学习技术和生存模型结合的方法：即通过将CoxPH model扩展到NN上，并移除其比例风险假定。并提供了其一个可用的基于pytorch的package —— pycox。

Methods

生存分析

对于某一event，其发生的时间\(T^*\)是一个随机变量： \[P(T^*\le t)=\int_0^tf(s)ds=F(t)\] 其中\(F(t)\)和\(f(t)\)分别是其density 和 cumulative distribution function。

对于\(F(t)\)，另一个可替代的、有实际意义的概念是survival function： \[S(t)=P(T^*\gt t)=1-F(t)\] 还有hazard function： \[h(t)=\frac{f(t)}{S(t)}=\lim_{\Delta t\to0}\frac{1}{\Delta t} P(t\le T^*\lt t+\Delta t|T^*\ge t)\]

通常来说，hazard function更加能够解释生存模型的本质，拥有明确的意义，而且其限制更少：（只需要保证非负和\(\int_0^{\infty}h(t)=\infty\)即可）。所以，大多数生存模型的建模是来对hazard function进行拟合。

进一步，我们可以得到cumulative function： \[H(t)=\int_0^th(s)ds\] 我们可以得到cumulative function和survival function以下的关系： \[S(t)=\exp[-H(t)]\]

在真实数据中，我们的随访时间不足以观察到时间的发生，这会造成right censor的出现，这时我们得到的时间为\(T=min\{T^*,C^*\}\)，其中\(C^*\)是censoring time，同时我们得到一个indicator \(D=\mathbb{1}\{T=T^*\}\)来指示时间\(T\)是否是一个censored data。

假设样本\(i\)拥有协变量\(\mathbf{x}_i\)和观测的时间\(T_i\)，我们有下面的likelihood：

\[L=\prod_i{f(T_i|\mathbf{x}_i)^{D_i}S(T_i)|\mathbf{x}_i}^{1-D_i} =\prod_i{h(T_i|\mathbf{x}_i)^{D_i}\exp[-H(T_i|\mathbf{x}_i)]}\tag{2}\]

或者称为full likelihood。

CoxPH 回归

Cox proportional hazards model【Cox, 1972】提供一个hazard function的半参数框架： \[h(t|\mathbf{x})=h_0(t)\exp[g(\mathbf{x})],\quad g(\mathbf{x})=\beta^T\mathbf{x}\tag{3}\]

其中\(h_0(t)\)称为non-parameteric baseline hazard，\(\exp[g(mathbf{x})]\)称为relative risk function。注意，这里没有intercept，其可以被包括进baseline hazard中。

整个模型的拟合分为两个部分：

首先使用partial likelihood来求解relative risk function部分：

\[L_{cox}=\prod_i(\frac{\exp[g(\mathbf{x}_i)]}{\sum_{j\in\mathcal{R}_i}\exp[g(\mathbf{x}_j)]})^{D_i}\tag{4}\] 其中\(\mathcal{R}_i\)表示那些在\(T_i\)时刻还处于风险中的个体组成的集合（即在\(T_i\)时刻还没有发生event而且没有删失的个体）。

进一步，可以得到其negative partial log-likelihood作为loss function： \[loss=\sum_i{D_i\{\log(\sum_{j\in\mathcal{R}_i}\exp[g(\mathbf{x}_i)])-g(\mathbf{x}_i)\}}\tag{5}\]

假设最后得到的参数的估计值为\(\hat{\beta}\)。
第二步，使用Breslow estimator来得到cumulative baseline hazard function：

\[\hat{H}_0(t)=\sum_{T_i\le t}\Delta\hat{H}_0(T_i)\\ \Delta\hat{H}_0(T_i)=\frac{D_i}{\sum_{j\in\mathcal{R}_i}\exp[\hat{g}(\mathbf{x_j})]}\tag{6} \]

如果可以，我们可以进一步通过平滑\(\hat{H}_0\)的增量来得到\(\hat{h}_0\)，但通常来说\(\hat{H}_0\)已经能够提供我们足够的信息了。

通过最大化式2，并将\(h_0(t)\)看做是piecewise constant between uncensored failure times得到。

Cox with SGD

Cox partial likelihood的优化一般使用Newton-Raphson's method，但利用minibatch SGD来优化的思路是非常简单的，即计算每个minibatch的loss优化即可，这和其他的loss的优化没有区别。

这对于满足比例假设的loss（DeepSurv）优化是没有问题的，但如果用于后面的非比例假设的loss的优化，将造成比较大的计算量，所以这里试图来得到一个该loss的估计值，更加容易在batches上进行计算。

首先，假设使用一个risk set\(\mathcal{R}_i\)的一个足够大的子集\(\tilde{\mathcal{R}}_i\)来估计partial likelihood已经足够，这里还使用了一个weight来保证其足够大：

\[L=\prod_i(\frac{\exp[g(\mathbf{x}_i)]}{w_i\sum_{j\in\tilde{\mathcal{R}}_i}\exp[g(\mathbf{x}_j)]})^{D_i}\tag{7}\]
这里保证\(i\)总是属于\(\tilde{\mathcal{R}}_i\)的。注意，在计算梯度的时候，\(w_i\)会被约去，所以其没有必要存在于loss中。另外\(D_i=0\)的项也对loss没有贡献。之后，我们再除以样本的数量，得到：

\[loss=\frac{1}{n}\sum_{i:D_i=1}\log(\sum_{j\in\tilde{\mathcal{R}}_i}\exp[g(\mathbf{x}_j-\mathbf{x}_i)])\tag{8}\]
在后面的实验中，我们发现，\(\tilde{\mathcal{R}}_i\)只有一个\(j\)已经足够，所以我们得到：

\[loss=\frac{1}{n}\sum_{i:D_i=1}\log(1+\exp[g(\mathbf{x}_j)-g(\mathbf{x}_i)]),\quad j\in\mathcal{R}_i\backslash\{i\}\tag{9}\]

注意，式8比式5更加易于理解，因为式8固定了risk sets的大小，从而使得值可以进行比较。式9的值的范围可以进行计算：\((0, 0.693]\)。

其实risk set的sampling可以在流行病学研究中被设计，通过nested case-control design。其中，case即\(i\)，而controls即\(j\)。【Goldstein and Langholz (1992)】已经证明了对于CoxPH，sampled risk sets给出了一致的参数估计，虽然此没有在non-linear models中得到证明，但式8作为一个loss function是合理的。

非线性的Cox

这里使用NN来构建\(g(\mathbf{x})\)，而likelihood和loss都不需要改变。

之后，case-control近似得到的loss（式8）使用Cox-MLP（CC）来代表，而使用原始的loss（式5）的使用Cox-MLP（DeepSurv）来代表。

对于非线性模型，loss并不能保证存在唯一的解，所以这里还需要加入一个惩罚以保证输出不能距离0太远：

\[penalty=\lambda\sum_{i:D_i=1}\sum_{j\in\tilde{\mathcal{R}}_i}|g(\mathbf{x}_j)|\]

这个问题在实践中碰到过。

非比例假设的Cox-Time

传统处理非比例假设的模型，做法是将将协变量分层，然后在每一层分别拟合cox模型【Klein and Moeschberger, 2003, chap. 9】，而这里我们使用参数化的方法来实现这一功能：

\[h(t|\mathbf{x})=h_0(t)\exp[g(t,\mathbf{x})]\]

即将时间当做一个协变量加入模型中。

以上模型有类似的loss function：

\[loss=\frac{1}{n}\sum_{i:D_i=1}\log(\sum_{j\in\tilde{\mathcal{R}}_i}\exp(g(T_i,\mathbf{x}_j)-g(T_i,\mathbf{x}_i)))\tag{12}\]

同样，式10的penalty也要用到，只是用\(g(T_i,\mathbf{x}_j)\)来替换\(g(\mathbf{x}_j)\)，这个模型称为Cox-Time。

主要，因为在loss中对于\(\mathbf{x}_i\)和\(\mathbf{x}_j\)都是使用\(T_i\)进行计算，所以如果使用式5进行计算，则时间复杂度是\(O(n\cdot|\mathcal{R}_i|)=O(n^2)\)。而如果使用式12进行计算，因为\(|\tilde{\mathcal{R}}_i|\)是一个固定的数，所以时间复杂度是\(O(n)\)。

对于传统的CoxPH，因为可以只计算\(g(\mathbf{x}_j)\)一次，然后在计算risk sets复用，所以其时间复杂度也是\(O(n)\)。

之后我们可以继续使用式6来对cumulative baseline hazard进行估计。

预测

对于比例假设的模型，可以使用下面的公式来预测生存函数：

\[\hat{S}(t|\mathbf{x})=\exp[-\hat{H}(t|\mathbf{x})]= \exp[-H_0(t)\exp(g(\mathbf{x}))]\]

而对于非比例假定的模型，因为relative risk function部分也依赖于时间，所以必须用下面的方法来估算：

\[\begin{aligned} H(t|\mathbf{x})&=\int_0^t{h_0(s)\exp[g(s,\mathbf{x})]ds} \\ &\approx\sum_{T_i\le t}{\Delta \hat{H}_0(T_i)\exp[\hat{g}(T_i,\mathbf{x})]} \\ \Delta\hat{H}_0(T_i)&=\frac{D_i}{\sum_{j\in\mathcal{R}_i}\exp[\hat{g}(T_i,\mathbf{x}_j)]} \tag{13} \end{aligned}\]

Evaluation Criteria

Concordance Index

C-Index【Harrell Jr et al., 1982】和ACC、AUC有着密切的关系【Ishwaran et al., 2008，Heagerty and Zheng, 2005】。简单来说，其估计了一个概率：对于随机的一对样本pair，其预测的生存时间和真实的生存时间顺序相关的概率。

因为C-index只依赖于预测的顺序，所以对于CoxPH model，因为其顺序不会依赖于时间的改变，所以使得使用relative risk function就可以进行评价。

然后对于非比例假设的模型，就必须使用time-depend C-index【Antolini et al. (2005)】，其估计了观测\(i\)和\(j\)在“可比”的前提下是“一致”的概率：

\[C^{td}=P\{\hat{S}(T_i|\mathbf{x}_i)\lt\hat{S}(T_i|\mathbf{x}_j)|T_i\lt T_j,D_i=1\}\]

另外还进行了【Ishwaran et al. (2008, Section 5.1, step 3)】的修改，为了能够保证当预测独立于协变量\(\mathbf{x}\)时，得到\(C^{td}=0.5\)。

Brier Score

BS本来是对于二分类的一个评价指标：

\[BS=\frac{1}{N}\sum_i(y_i-\hat{p}_i)^2\] 其中\(y_i\)是标签，\(\hat{p}_i\)是预测的概率。

【Graf et al. (1999)】将Brier score扩展到了time-to-event data领域：

\[BS(t)=\frac{1}{N}\sum_i^N[ \frac{\hat{S}(t|\mathbf{x}_i)^21\{T_i\le t,D_i=1\}}{\hat{G}(T_i)}+ \frac{(1-\hat{S}(t|\mathbf{x}_i))^21\{T_i\gt t\}}{\hat{G}(t)}]\]

其中\(N\)是观测的数量，\(\hat{G}(t)\)是censoring survival function的Kaplan-Meier估计 \(P(C^*\lt t)\)（即将删失作为event构建的生存函数），这里假设censor和event是独立的。

BS可以进一步扩展为integrated Brier score：

\[IBS=\frac{1}{t_2-t_1}\int_{t_1}^{t_2}{BS(s)ds}\]

实践中，一般将区间进行分块来近似计算这个积分（100个分割点足够了）。

Binomial Log-likelihood

\[BLL(t)=\frac{1}{N}\sum_{i=1}^N[ \frac{\log[1-\hat{S}(t|\mathbf{x}_i)]1\{T_i\le t,D_i=1\}}{\hat{G}(T_i)} + \frac{\log[\hat{S}(t|\mathbf{x}_i)]1\{T_i\gt t\}}{\hat{G}(t)} ]\]

同样的，可以得到一个integrated version：

\[IBLL=\frac{1}{t_2-t_1}\int_{t_1}^{t_2}{BLL(s)ds}\]

Simulation

模拟以验证以上提到的算法是否可行。classical cox使用Lifelines packages来实现。

这里简单介绍以下模拟的方法：

假设我们的模型有下面的形式： \[h(t|\mathbf{x})=h_0(t)\exp[g(t,\mathbf{x})]\] \(H(t|\mathbf{x})=\int_0^t{h(s|\mathbf{x})ds}\)是连续的累积风险函数，\(V\)是参数为1的指数分布（\(P(V\gt v)=\exp(-v)\)）。则我们可以通过下面的公式来采样得到符合上述累计风险函数的生存时间：

\[T^*=H^{-1}(V|\mathbf{x})\]

因为\(S(t|\mathbf{x})=P(T^*\gt t|\mathbf{x})=P(H^{-1}(V|\mathbf{x})\gt t)=P(V\gt H(t|\mathbf{x}))=\exp[-H(t|\mathbf{x})]\)

为了能够构造出\(H^{-1}\)，所以一般需要\(g(t,\mathbf{x})\)简单一些。

模拟探索损失函数8的行为

首先，我们探索loss function 8的行为，即不同controls samples的数量的结果和使用正常的偏似然函数（loss 5）之间的差别。

模拟数据来自proportional hazards model： \[h(t|\mathbf{x})=h_0(t)\exp[g(\mathbf{x})]\\ g(\mathbf{x})=\beta^T\mathbf{x}\] 其中使用constant baseline hazard \(h_0(t)=0.1\)和\(\beta=[0.44,0.66,0.88]^T\)，协变量采样自\(\mathcal{U}(-1, 1)\)。censoring time来自constant hazard \(c(t)=\frac{1}{30}\)，其和协变量的采样是独立的，并设置了截止时间为30。以上的设置大约导致了30%的删失。然后采样了10000个样本作为training，10000个样本作为test。

使用loss function 8中描述的方式来拟合Cox model（称为Cox-SGD），四个模型分别是control 采样数为1, 2, 4, 8。所有的实验都重复了100次，test中的mean partial log-likelihood（MPLL）作为评价指标，结果如下图：

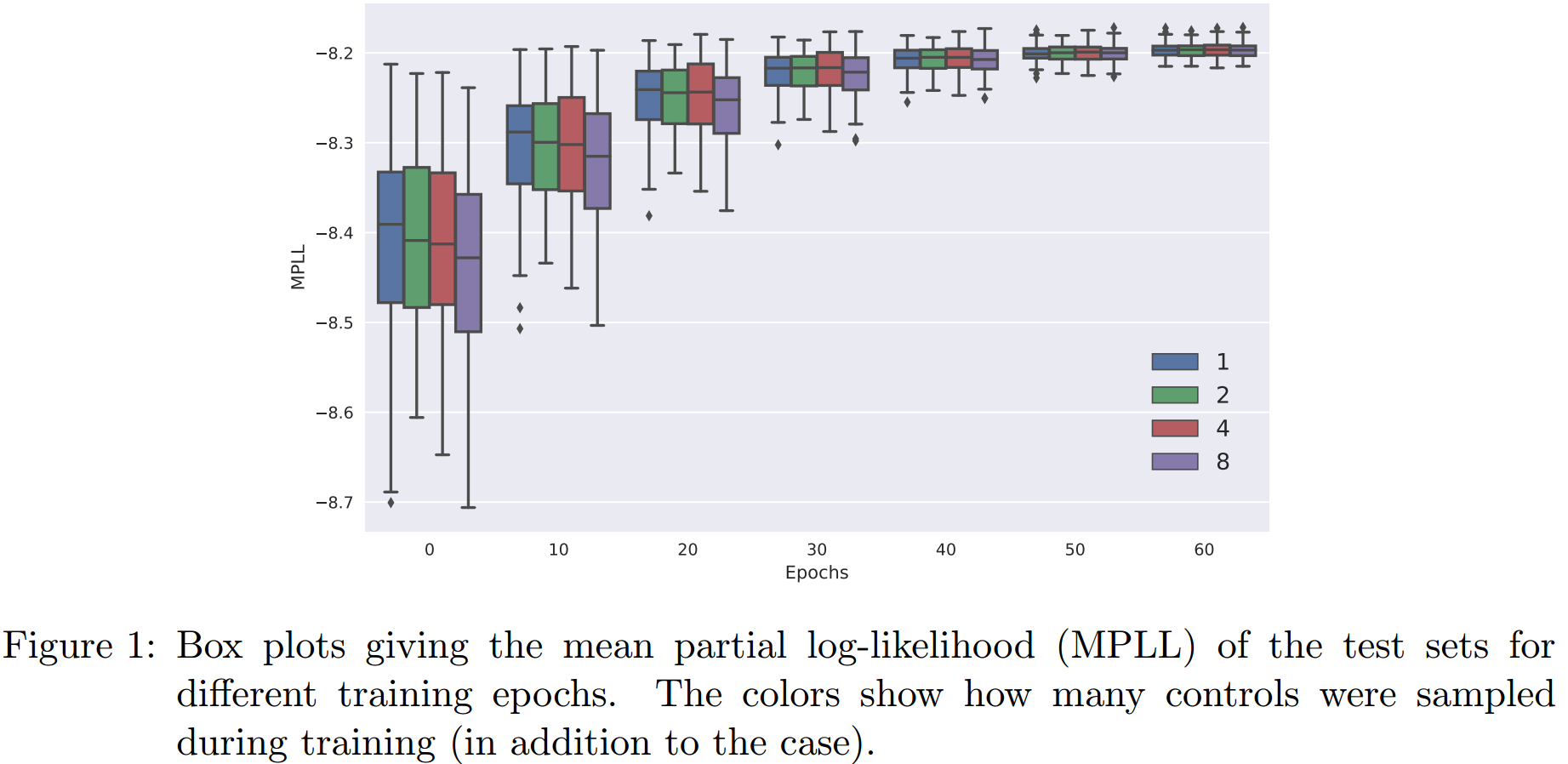
我们可以看到，其对于收敛的速度并没有影响，但采样数量越多会带来更大的计算复杂度。之后，为了证明样本量的减少不会影响模拟结果，使用1000个样本的training也进行了相同的实验，其结果与上图基本一致。

接下来，我们比较一下cox-SGD所拟合的参数和classical cox所拟合参数的不同。结果展示在下图中：

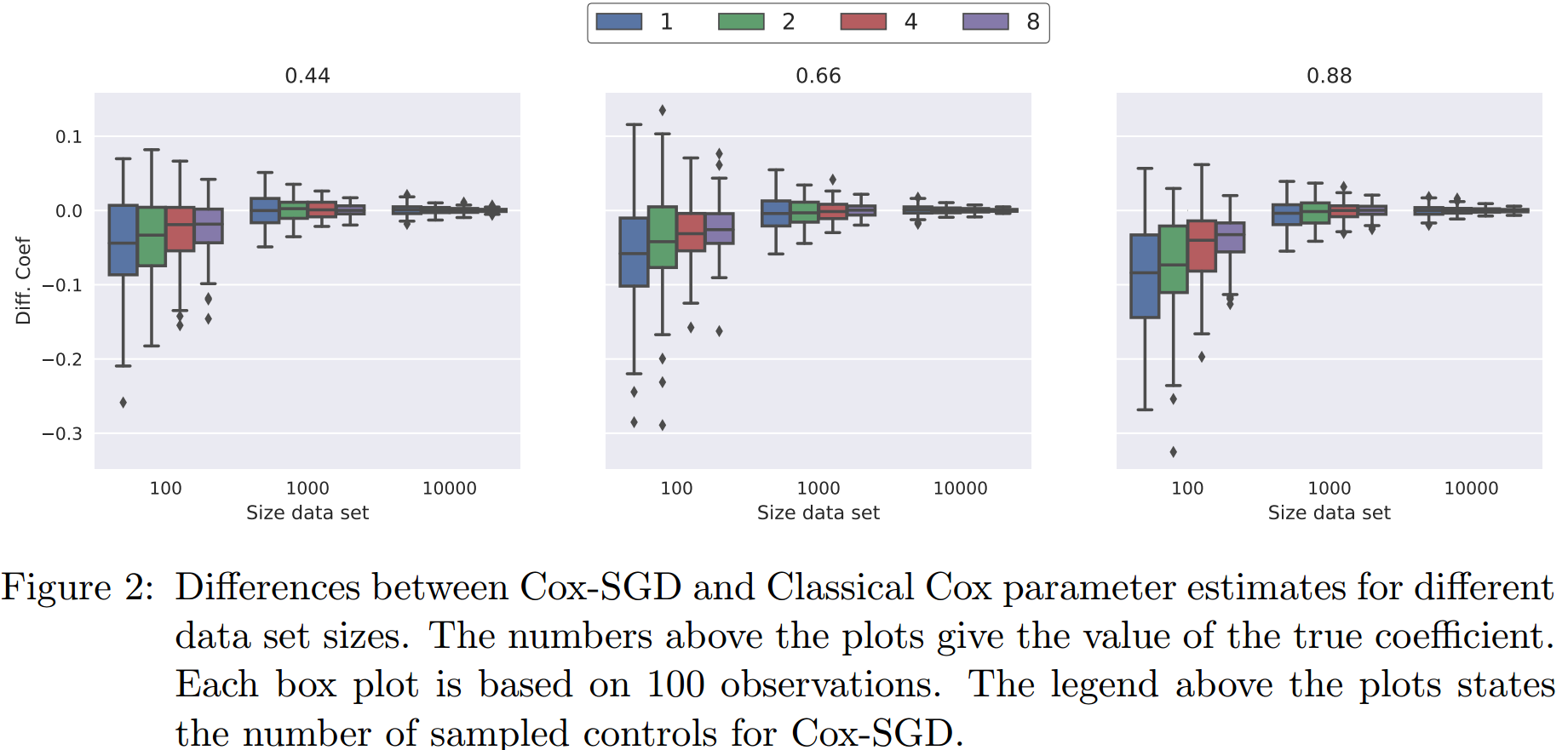
在样本量较少的时候，cox-SGD拟合的参数要小一些，而且似乎control采样数越少，这个趋势越明显。但随着样本量的增加，这个基本就不存在了。

最后，我们想要比较一下两个方法likelihood（full likelihood，式2）的差别。这里看的是training的likelihood，因为我们只想知道不同的方法的优化能力，而非模型的泛化能力。结果如下图所示：

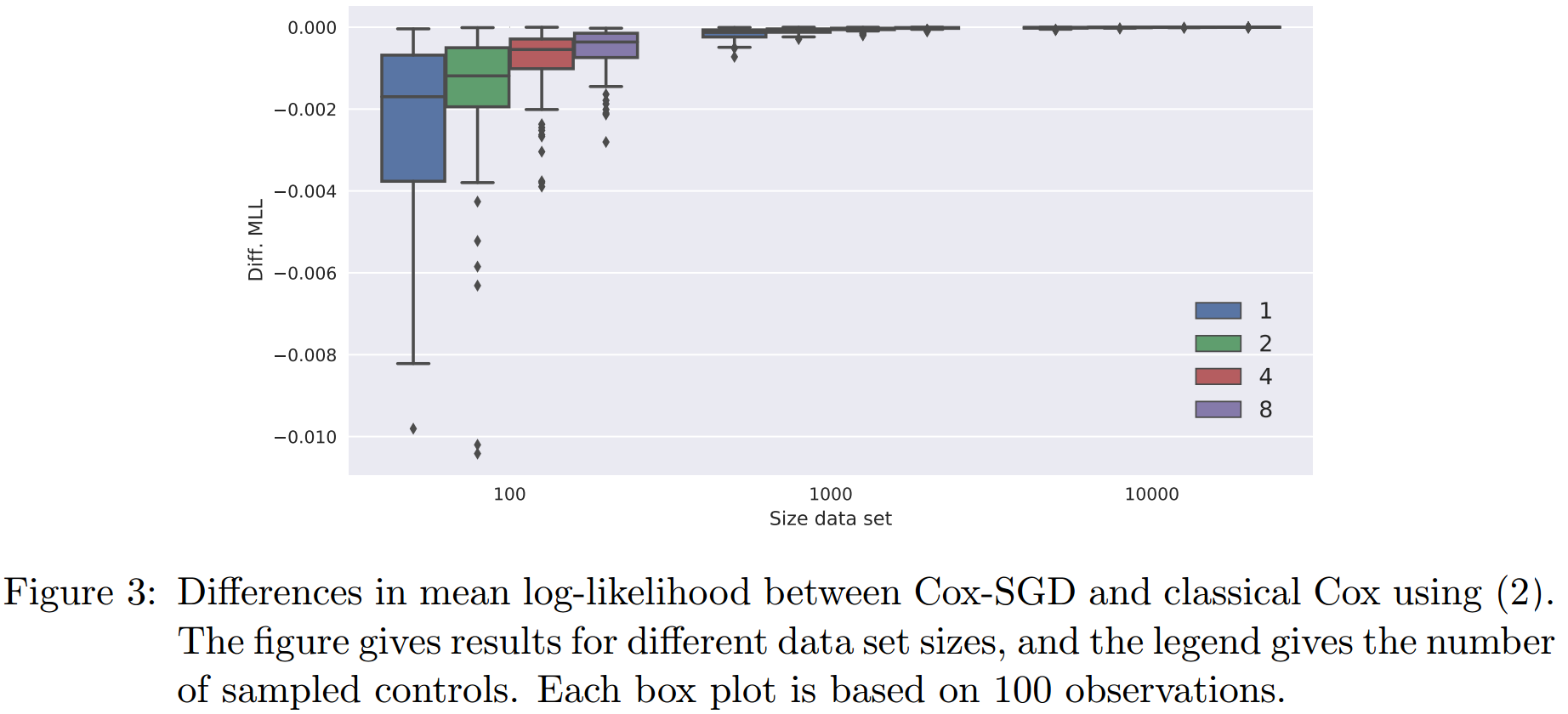
可以看到，似乎control采样数越多，cox-SGD的结果越接近classical cox，但随着样本的增加，两者的差距缩小。classical cox的MLL大约是-2.2作用，所以即使对于最小样本量下，cox-SGD所带来的影响也小于0.1%，所以这也说明了该方法的有效性。

非线性和非比例假设模型

该内容在Appendix C。

非线性模型：

\[g(\mathbf{x})=\beta^T\mathbf{x}+\frac{2}{3}(x_1^2+x_3^2+x_1x_2+x_1x_3+x_2x_3)\]

cox-MLP使用的是1-hidden layer（64个节点）的模型，然后绘制了其和cox-SGD在2000个test点上的PLL散点图：

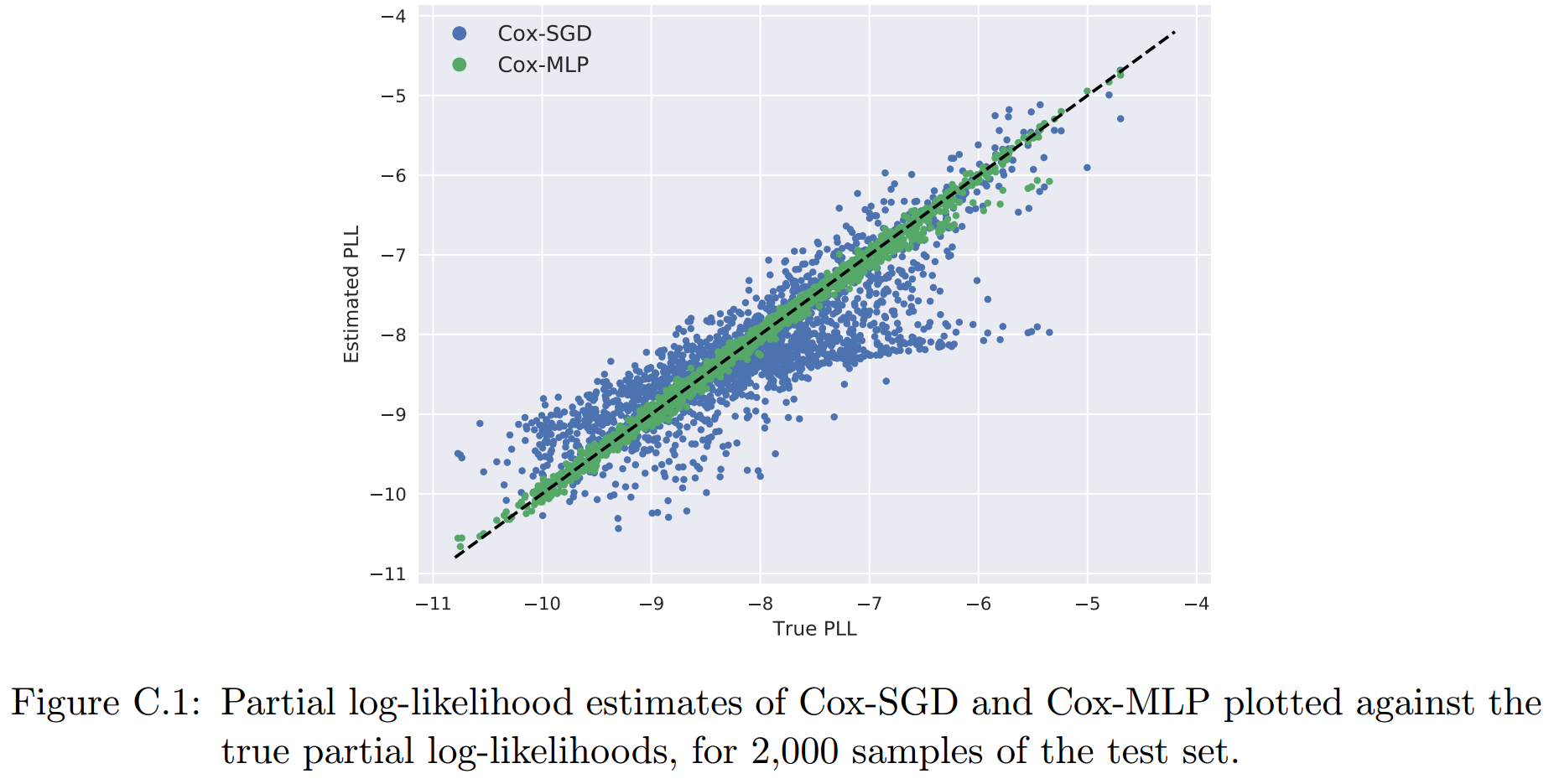
可以看到对于非线性问题，Cox-MLP有着更好的结果。

非比例假设模型：

\[ g(t,\mathbf{x})=a(\mathbf{x})+b(\mathbf{x})t,\\ a(\mathbf{x})=g_{ph}(\mathbf{x})+sign(x_3),\\ b(\mathbf{x})=|0.2(x_0+x_1)+0.5x_0x_1| \]

cox-MLP和cox-Time都是用4-hidden layer的NN，每个layer是128个节点，dropout rate是0.1。其PLL的散点图为：

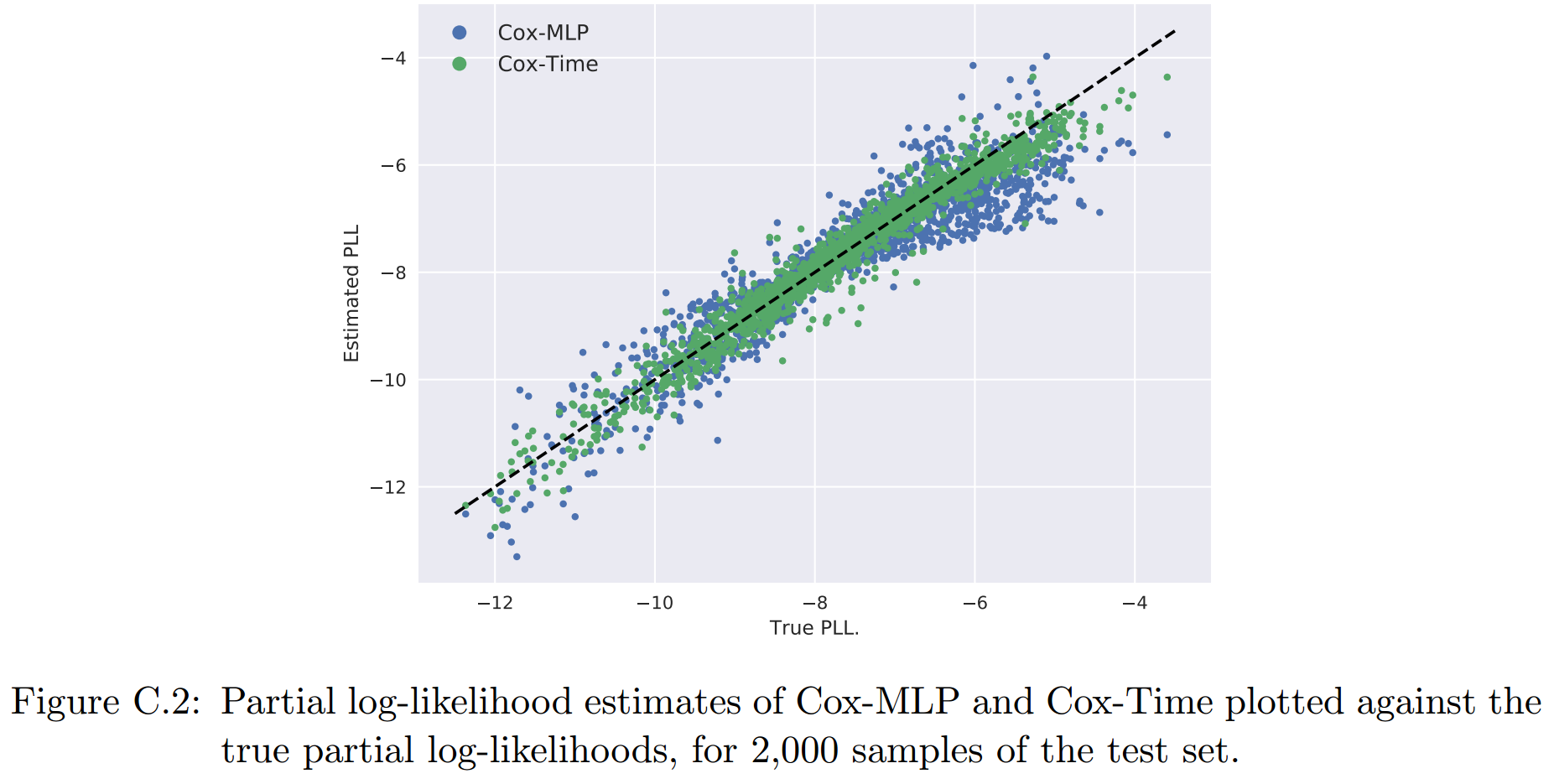
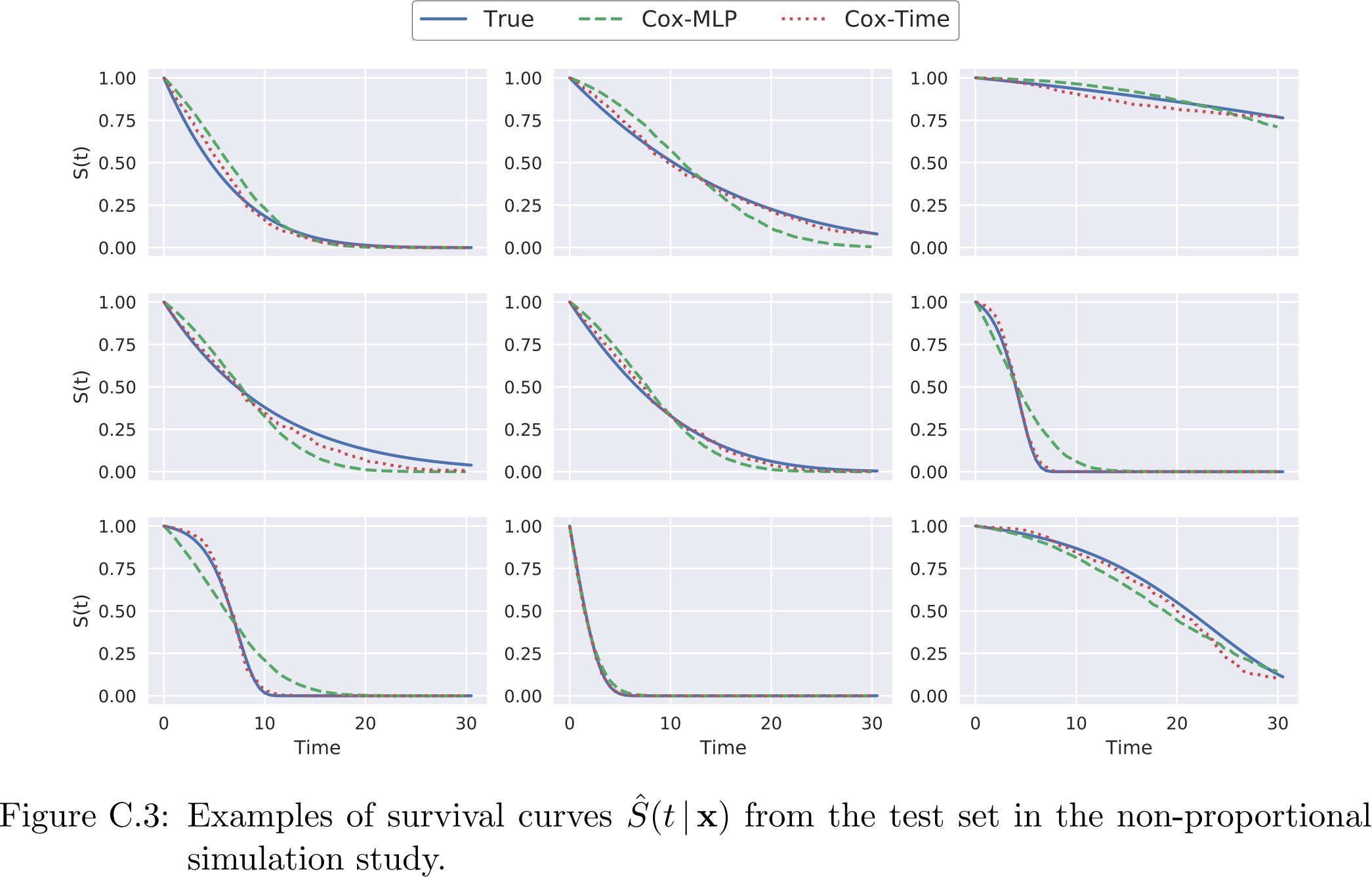
进一步，我们绘制了几个样本的生存曲线，可以看到，Cox-Time拟合的效果要好于Cox-MLP：

Experiments

本部分，将使用真实数据来比较各类模型的表现。

小规模数据集实验

使用数据集

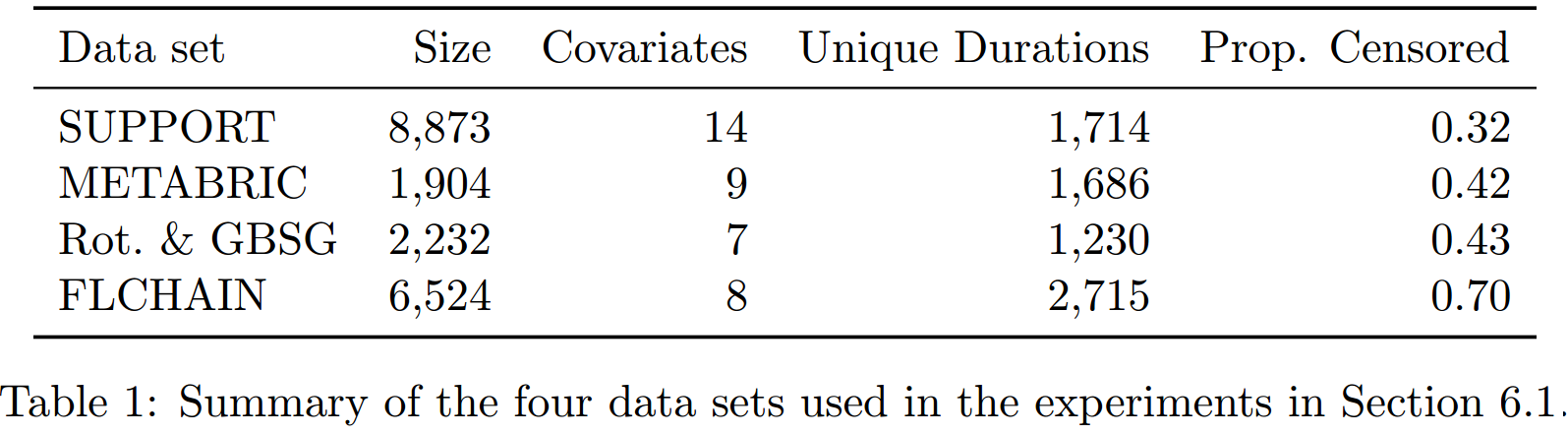
前三个来自【Katzman et al. (2018)】，由DeepSurv python package提供。最后一个有R package survival提供（移除了chapter协变量）。

使用的方法

使用control sampling的proportional Cox method：Cox-MLP(CC)
使用control sampling的non-proportional Cox method：Cox-Time
Classical Cox（linear）
DeepHit
Random Survival Rorests（RSF）
Cox-MLP（MLP），此方法与DeepSurv的不同在于使用的是minibatch SGD来训练，使用的loss是式5

关于数据集的处理：

对于使用NN的方法，我们首先将协变量标准化，然后使用entity embedding的方法将分类协变量变为长度是其类别数一半的向量【Guo and Berkhahn, 2016】。
对于Classical Cox（linear），分类协变量是one-hot的。
对于RSF，协变量不做任何处理。

对于NN的架构：

所有的NN使用相同的架构，每一层有相同的节点数、ReLU激活、BN。
使用了dropout、normalized decoupled weight decay【Loshchilov and Hutter, 2019】和early stopping来进行正则化。
SGD的方法是AdamWR【Loshchilov and Hutter, 2019】，并使用【Smith (2017)】的方法来找到学习率。

整个验证过程：

5-CV。
对于NN，每一折中，都对总共300多对参数组合进行random hyperparameter search，找到最优的参数组合，这里使用的评价指标是partial log-likelihood（比例假定的模型）和式12（Cox-Time）。
而DeepHit和 RSF的超参数调整使用的是time-dependent c-index【Antolini et al., 2005】。我们也使用了RSF作者建议的超参数调整方法，即通过计算concordance of the mortality【】，这两种方法得到的模型分别称为RSF（\(C^{td}\)）和RSF（Mortality）。

这里使用的超参数的设置可以参见Appendix A1部分。

结果

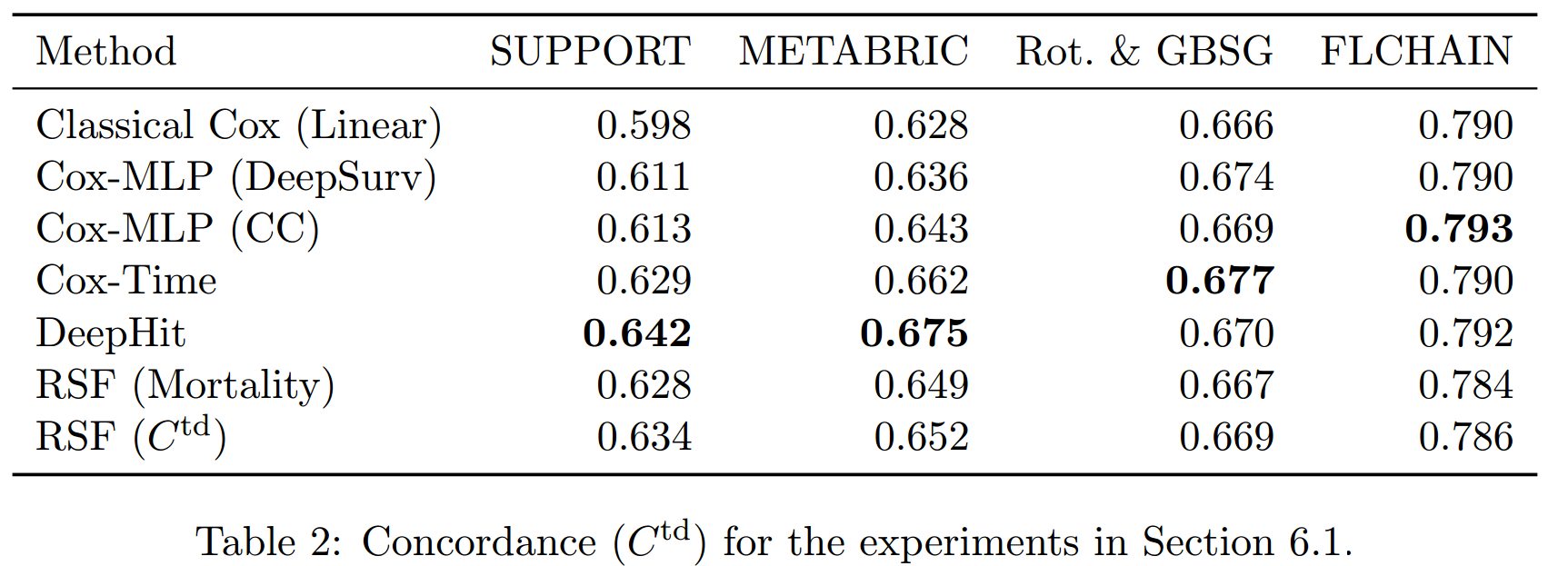
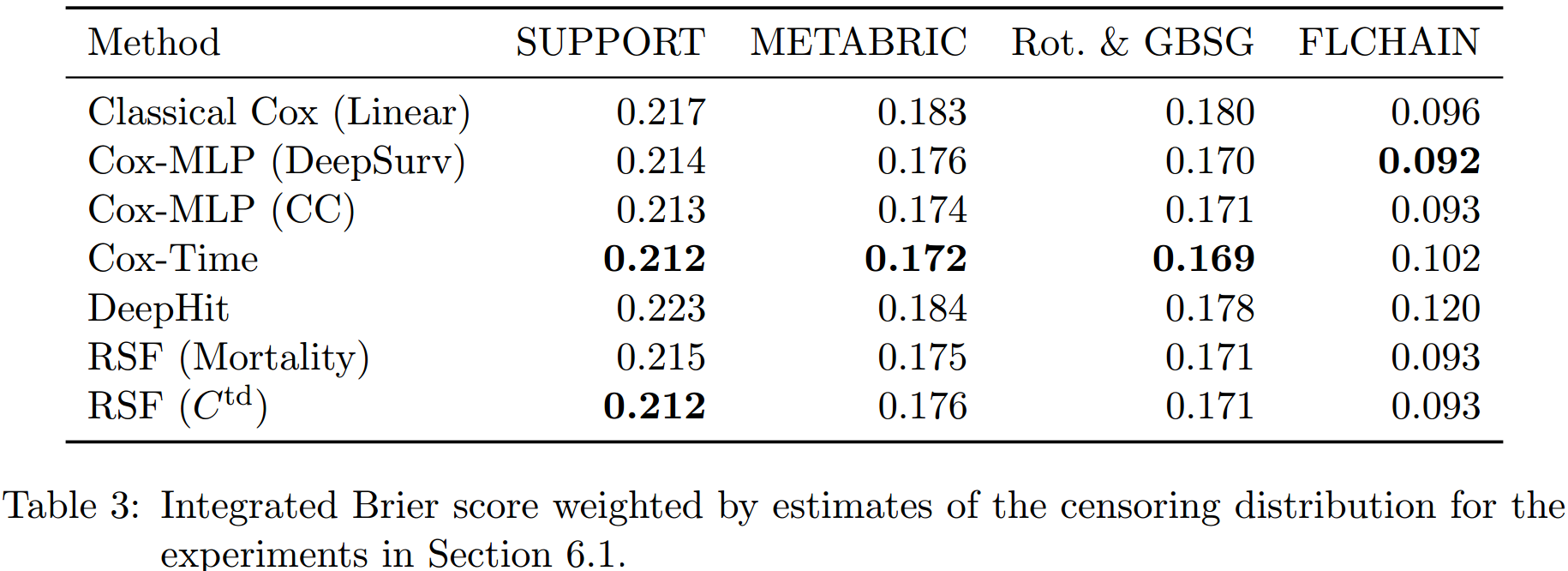
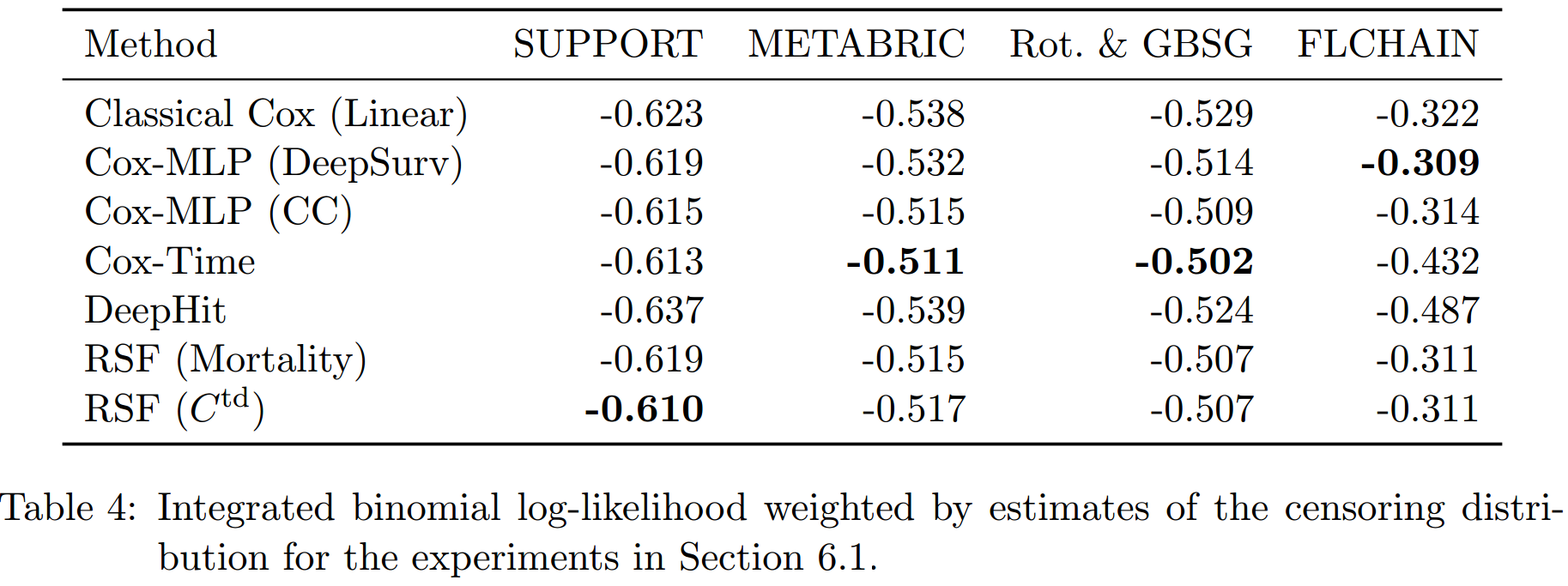
以上的3个tables展示了3种评价指标的结果：

在C-index上，非比例假设的模型的结果要普遍好于比例假设的模型。RSF（\(C^{td}\)）要好于RSF（Mortality），这可能是因为前者就是使用C-index来进行超参数调整的原因。而总的看来，Cox-Time的效果要略好于RSF，尽管其并不是使用C-index来进行的超参数调整。总的来说，似乎DeepHit表现最好，但这是其以其低效的生存预测为代价所得到的。

注意，C-index高只需要保证顺序对就可以，其生存函数的预测可能是非常差的。
在IBS和IBLL上，前三个数据集上Cox-Time都表现很好，在最后一个数据集上反而是以CC和DeepSurv为最高，这说明比例假定可能在此数据集上更加合适。

而在这两个指标中，DeepHit的表现不好。从其loss的形式中可以看出，其综合了两方面：negative log-likelihood和ranking loss，并使用一个超参数\(\alpha\)来进行调节。超参数搜索得到的\(\alpha\)都偏小，即更加便偏向于使用ranking loss的部分来进行拟合，从而其得到了较好的C-index，但拟合的生存函数较差。

大样本数据集实验

数据集

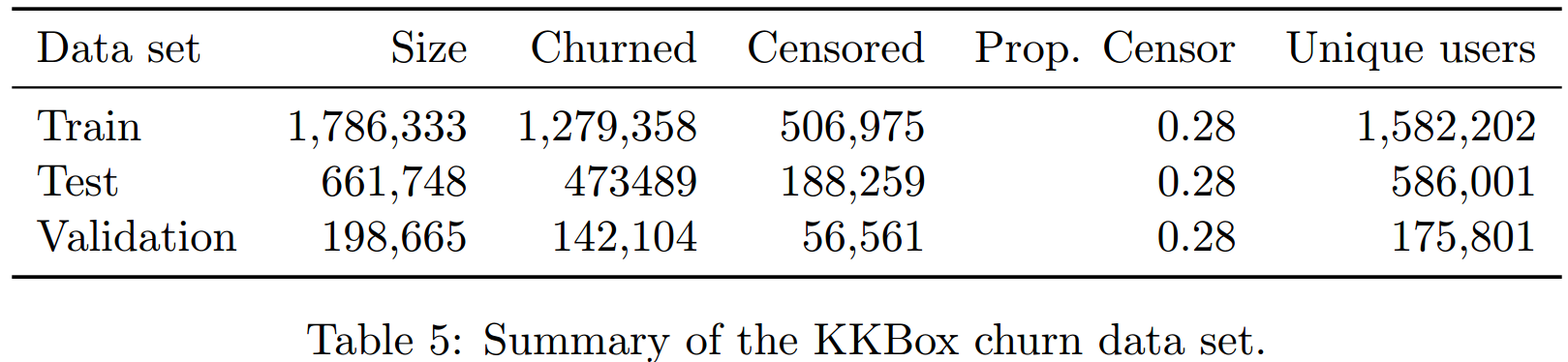
WSDM KKBox's churn prediction challenge由Kaggle在2017年举办，为了预测音乐流媒体的客户流失现象。

如果一个客户在上次订阅后30天内没有续订，则认为此客户流失了，这是我们的event。协变量只使用最基础的那些（共有15个）。有些客户可能在流失后又续订，这被看做是一个新的样本。最终数据集被分为train、valid和test，详细信息如上表所示。

关于此数据集的详细信息可见Appendix B1部分。

方法

使用的方法和“小样本数据集实验”中一致，但因为样本量太大，所以将classical cox替换为cox-SGD（linear）。

训练NN时将学习率乘以0.8，为了稳定训练。

因为样本量非常大，所以在进行超参数搜索的时候，不再包括weight decay，只是在一个小数量的合适的参数中寻找。找到的最优参数组合是：

至于RSF，基于\(C^{th}\)的模型发现每次split采样8个协变量、每个叶节点最少50个样本，基于mortality的模型发现每次split采样2个协变量、叶节点的size最小是10。500个trees足够，但其和250个trees的结果没有什么差别。

这里使用的超参数的设置可以参见Appendix A2部分。

结果

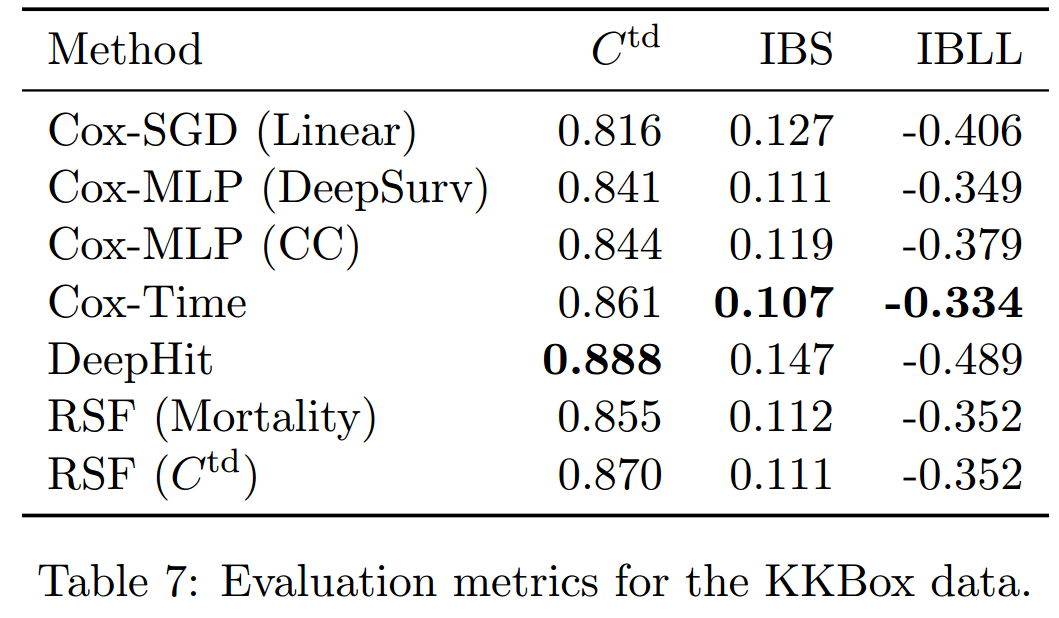
每类模型都拟合5次，并将得到的评价指标的均值作为最后的结果。可以看到，趋势和小样本时是相似的。

之后，我们将每个时间点的BS计算出来（注意，这里越小越好）：

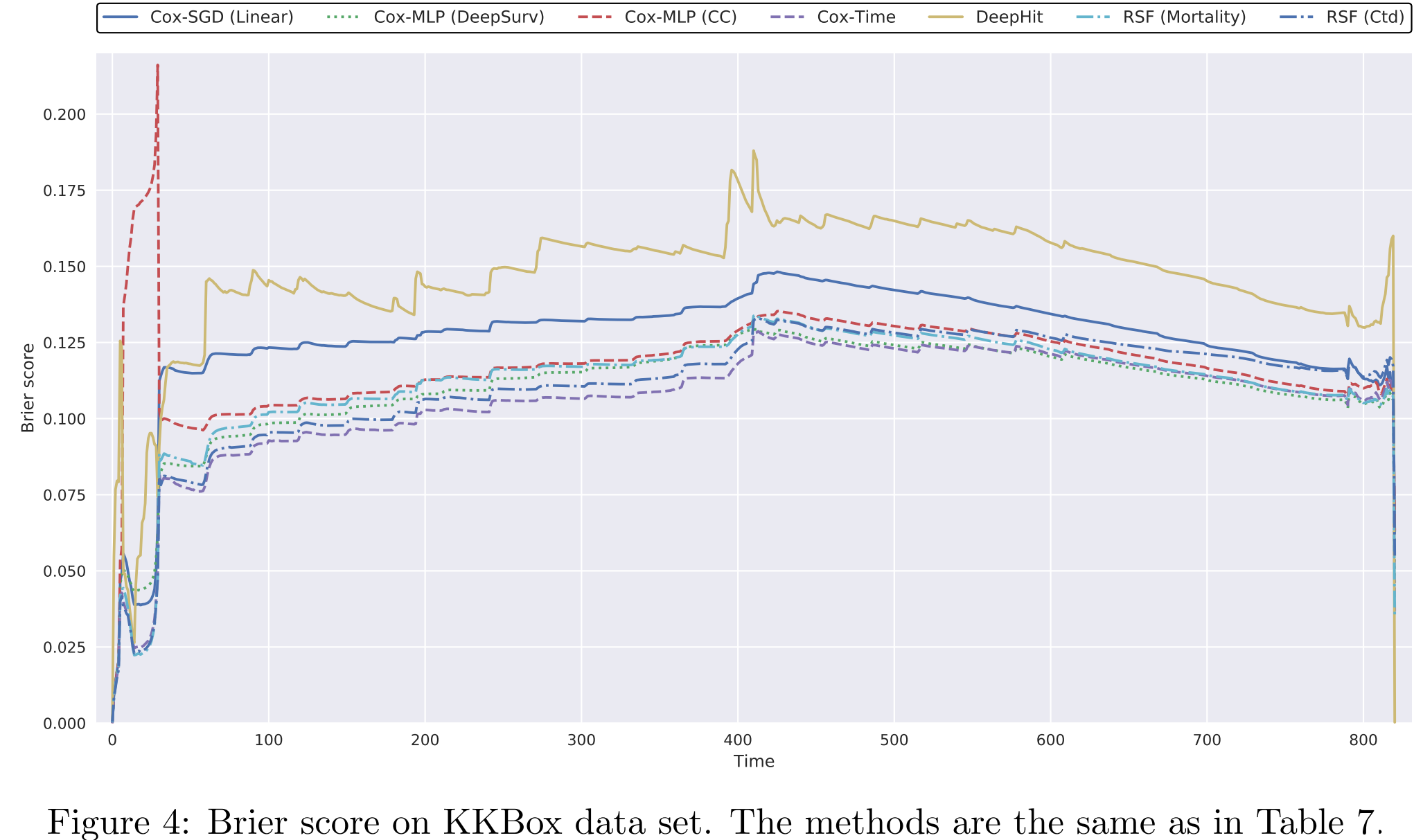
这里可以看到，依然是DeepHit是最差的，Cox-Time是最好的。Cox-MLP(DeepSurv)在长时间的预测中表现最好。BLL的图像和BS非常类似。

生存曲线

生存分析相对于分类任务的一个优势就是，可以给出生存曲线，有着更强的解释性。比如下面是Cox-Time在test上9个样本上的估计生存曲线：

为了能够对预测有更加general的视角，这里我们将test的预测生存曲线进行聚类。每个样本预测\(0=\tau_0\lt\tau_1\lt\cdots\lt\tau_m\)这些时间点上的生存概率，然后将其作为feature进行k-means聚类，聚类数为10。各类的生存曲线在下图中：

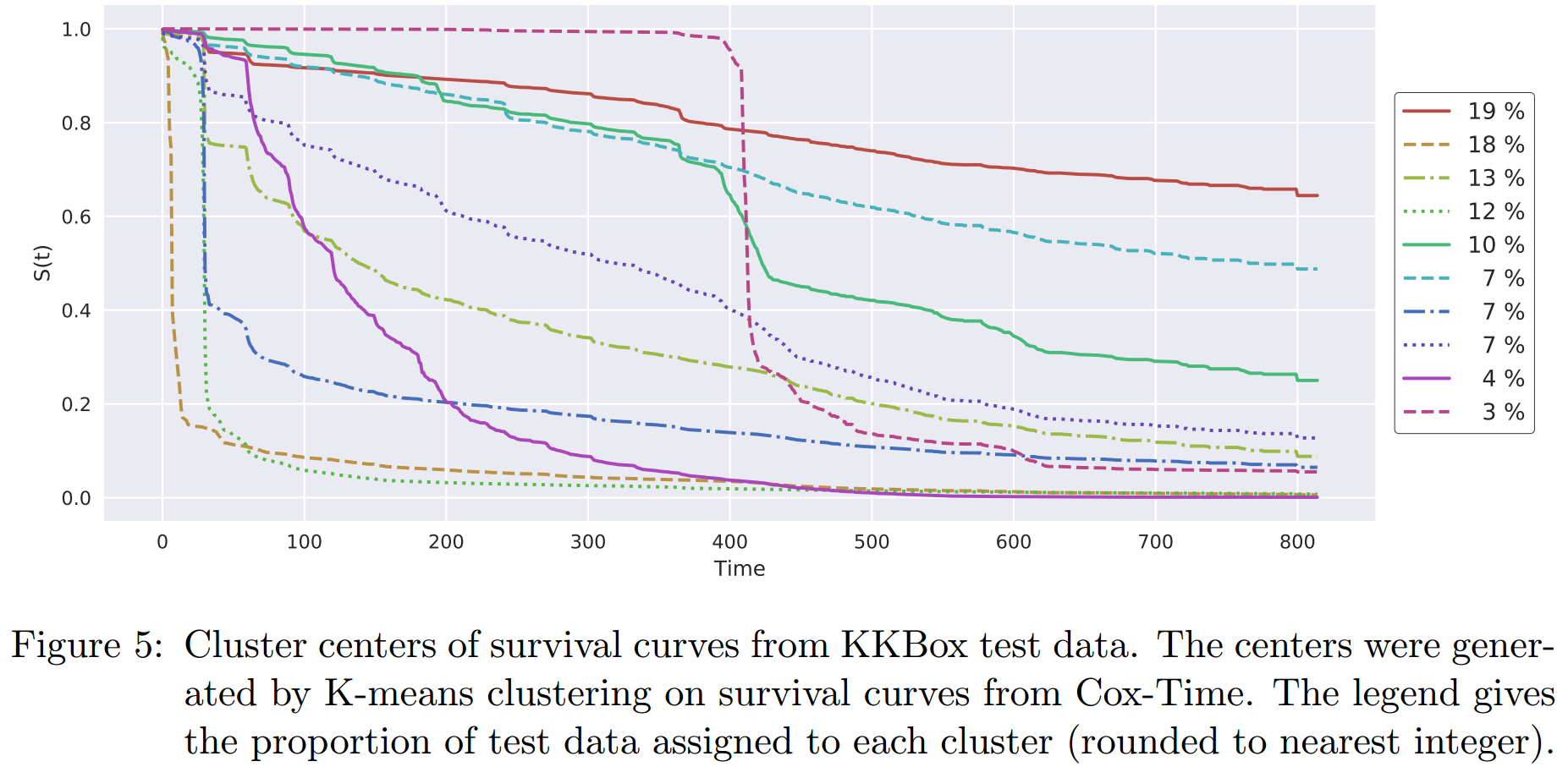
我们可以看到：

第一大类（19%的样本）是一条非常稳定的曲线
第二大类（18%）则有着非常高的脱落的风险
许多曲线没30天都有一次波动，这可能是因为月底付费所导致的
最少的那一类，则是在预定大约400天后急剧下降，查询他们的数据可以知道，这一类人大多在订阅400天后不再订阅。

Questions

Luyiyun

https://luyiyun.online/2020/10/12/paper/omics/paper-nnandcox-2019/

本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 Luyiyun !

Deep Learning Survival Analysis

论文精读-使用神经网络进行Time-to-Event预测-2019

Time-to-Event Prediction with Neural Networks and Cox Regression

Introduction

相关工作

Methods