Axiomatic Attribution for Deep Networks
- 杂志: None
- IF: None
- 分区: None
- github
Introduction
研究的问题是将NN的输出归因于其输入特征。
定义1:假设有function \(F:\mathbb{R}^n\to[0,1]\)是一个NN,其输入是\(x=(x_1,\dots,x_n)\),预测在\(x\)上相对于基线输入\(x'\)的attribution是\(A_F(x,x')=(a_1,\dots,a_n)\in\mathbb{R}^n\),其中\(a_i\)是\(x_i\)对于预测\(F(x)\)的贡献。
该问题已经在许多研究中被讨论过了【Baehrens et al., 2010; Simonyan et al., 2013;Shrikumar et al., 2016; Binder et al., 2016; Springenberg et al., 2014】。
这个工作的意义在于能够更加理解NN的行为,从而使得我们可能进一步对其进行改进。
Two Fundamental Axioms
Sensitivity。
一个attribution方法满足sensitivity即:如果某个feature的输入和其baseline产生了不同的预测,则此feature应该被给与非0的attribution。
梯度违背了sensitivity:比如有下面的网络\(f(x)=1-ReLU(1-x)\),baseline是\(x=0\),输入是\(x=2\),则函数从\(0\)变为\(1\),但梯度在\(x=2\)时是\(0\)。之所以出现这种情况,是因为梯度可能在input的那一点上是“平坦的”【Shrikumar et al., 2016】。这可能导致一些问题(fig2中的fireboat)。
已有的方法中,Deconvolution和guided back-propagation违反了sensitivity。DeepLift和LRP通过增加baseline和离散积分来避免违反sensitivity,但可惜的是,这些方法违反了另外一条重要的公理。
Implementation Invariance
如果两个网络对于所有的输入都得到相同的输出,则称这两个网络是functionally equivalent。“我们”认为attribution方法需要满足Implementation Invariance,即:对于两个functionally equivalent的NN,attribution需要相同。
Gradients是满足此性质的。
DeepLift和LRP之所以不满足此性质,是因为其使用的是离散梯度,而离散梯度并不符合链式法则,从而其得到不是真实的梯度,而真实的梯度是满足此性质的,所以其离散梯度反而不满足了。
相关工作
最早的工作之一是【Ribeiro et al., 2016a;b】,其试图使用一个简单的、可解释的模型在局部模仿NN,从而对其进行解释。这个思路无法实现Sensitivity,如果在局部是非常flat的,则这个方法会失效。而且该方法对于像图像这样dense的数据,计算量非常大。
注意力机制【Bahdanau et al., 2014】被期望能够有解释的能力,但就像LSTM中的门控单元一样,整个网络是复杂的,网络的其他部分可能会和注意力机制部分相互影响,单单考虑注意力机制可能并不能了解到全部的信息。
之前的一些基于扰动的方法【Samek et al., 2015】的缺陷在于:单纯对单个变量进行扰动对于NN这样复杂的模型并不适合,比如某个很重要的特征在被扰动的时候可能并不会导致预测性能的大量下降,因为其他特征可能会对其进行补偿。
还有一类方法需要借助人类为图像上的对象绘制标注框,然后计算标注框中像素的百分比。通常来说,图片上的对象是对预测最关键的内容,但在某些情况下也有可能是反的,背景反而提供了更多的信息。(fig2中的蝴蝶和卷心菜)
Methods
直观上,Integrated Gradients就是将Gradients的Implementation Invariance和DeepLift、LRP的Sensitivity结合在一起。
这里假设样本\(x\in\mathbb{R}^n\),baseline是\(x'\in\mathbb{R}^n\)(这个baseline在图像上可以black image,在text上就是zero embedding vector等)。然后,我们计算从baseline到\(x\)的直线路径上的梯度积分:
\[IntegratedGrads_i(x)=(x_i-x_i')\times\int_{\alpha=0}^1{\frac {\partial F(x'+\alpha\times(x-x'))}{\partial x_i}}\]
Integrated Gradient的性质
Completeness:
即attributions加起来等于\(F\)在\(x\)和基线\(x'\)的输出的差,数学语言描述为:
如果\(F:\mathbb{R}^n\to\mathbb{R}\)是几乎处处可微的,则\[\sum_{i=1}^n {IntegratedGrads_i(x)}=F(x)-F(x')\]
我们首先需要回顾一下“方向导数”的定义:\[F_{\overrightarrow{r}}'(x)= \lim_{\Delta\alpha\to0}\frac{F(x+\Delta\alpha\overrightarrow{r}) -F(x)}{\Delta\alpha}=F'(x)\cdot\overrightarrow{r}\] 其中\(F'(x)\)是\(F\)在\(x\)上的梯度。现在我们对该定义进行一定的扩展,定义函数: \[F_{\overrightarrow{r},x}(\alpha)=F(x+\alpha\overrightarrow{r})\] 注意,这是一个一元函数,所以其导函数可以写成: \[F_{\overrightarrow{r},x}'(\alpha)= \frac{dF_{\overrightarrow{r},x}}{d\alpha}= F'(x+\alpha\overrightarrow{r})\cdot\overrightarrow{r}\] “方向导数”是该导函数在\(0\)时的值。 然后我们把上面的性质1的左侧写开: \[\begin{aligned} \sum_{i=1}^n{IntegratedGrads_i(x)}&= \int_{\alpha=0}^n{\sum_{i=1}^n{(x_i-x_i')F_i(x'+\alpha\times(x-x'))}d\alpha} \\ &=\int_{\alpha=0}^n{F'(x'+\alpha\times(x-x'))\cdot(x-x')d\alpha} \end{aligned}\] 可以发现积分式内就是上面的一元函数的导函数,所以直接使用微积分基本定理,得到结果。
如果满足这个性质,则我们可以选择一个baseline使得其预测基本接近\(0\)(比如在图像分类中的black image),这样attributions的和就等于该类的输出。
Completeness满足可以推出Sensitivity满足。
因为Integrated Gradients的计算只是基于梯度的计算,梯度满足Implementation Invariance,所以Integrated Gradients也满足此性质。
Integrated Gradients是唯一可选的
首先,我们来扩展Integrated Gradients,我们不再使用直线上的路径积分(如fig1所示)。
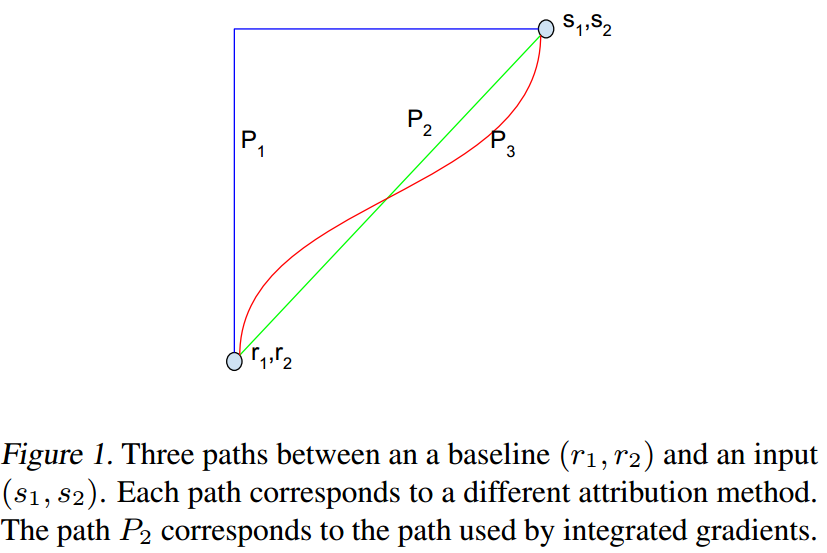
令\(\gamma=(\gamma_1,\dots,\gamma_n):[0,1]\to\mathbb{R}^n\)是一个光滑函数(即一个path),并且满足\(\gamma(0)=x',\gamma(1)=x\)。我们有下面的path integrate:
\[PathIntegratedGrads_i^{\gamma}(x)= \int_{\alpha=0}^1{\frac{\partial F(\gamma(\alpha))} {\partial\gamma_i(\alpha)}\frac{\partial\gamma_i(\alpha)} {\partial\alpha}d\alpha}\]
当\(\gamma(\alpha)=x'+\alpha\times(x-x')\)时,我们得到了Integrated Gradients。
可以知道:path method是满足Implementation Invariance的(只是利用了梯度);其也是满足Completeness,从而满足Sensitivity。
有意思的是,path method是满足另外一些性质的唯一的方法(证明见【Friedman, 2004】):
- Sensitivity(b),如果NN不依赖于某个变量,则在该变量上的attribution是0。
- Linearity,第三个NN由前两个NNs线性组合得到\(a\times f_1+b\times f_2\),则第三个NN的attributions是这两个NNs的attributions的线性组合,权重是\(a\)和\(b\)。
- Path methods是唯一满足Implementation Invariance、Sensitivity(b)、Linearity、Completness的attribution方法。
path integrated gradients方法很早就已经在经济学领域使用。
接下来,我们来叙述为什么使用直线路径是更合理的。
计算的简单。
保持对称性。
两个变量相对于函数\(F\)满足对称性即:\(F(x,y)=F(y,x),\quad \forall x,y\)。一个attribution方法是对称保持的,即对称变量如果有相同的输入和基线,则应该有相同的attribution值。
可以证明:
Integrated Gradients是唯一的保持对称的path method。
实际上,如果我们能够对多条path的结果进行平均,则该结果也是保持对称的,这一类方法在经济学领域也得到了广泛应用。但这在深度学习领域碰到的一个问题是:计算量太大。
实现
如何选择baseline:选择的baseline应该尽量保证其输出接近0。
当然,还可以有更好的选择。比如对于图像来说,black image和noise image其输出都是接近0的,但使用black image可能更加容易检测出边缘的特征。所以我们可以根据我们的目的来选择使用baseline。
如何计算:可以通过求和有效的来逼近计算积分。
\[IntegratedGrads_i^{approx}(x)= (x_i-x_i')\times\sum_{k=1}^m{\frac{\partial F(x'+\frac{k}{m}\times(x-x'))} {\partial x_i}\times\frac{1}{m}}\]
在实验中发现,\(m\in[20,300]\)就足够了。可以通过检查得到的attributions的和与输入和基线的预测差的差距来判断\(m\)是否合适。
Results
图像分类网络
这个网络是GoogleNet架构,在ImageNet object recognition datasets【Russakovsky et al., 2015】上进行的训练。使用Integrated Gradients计算attributions,其中只计算其中分类概率最高的那个类,使用的baseline是black image。
结果如下,其是在color channels上进行了聚合。可以看到,相比于gradients,其效果更好。

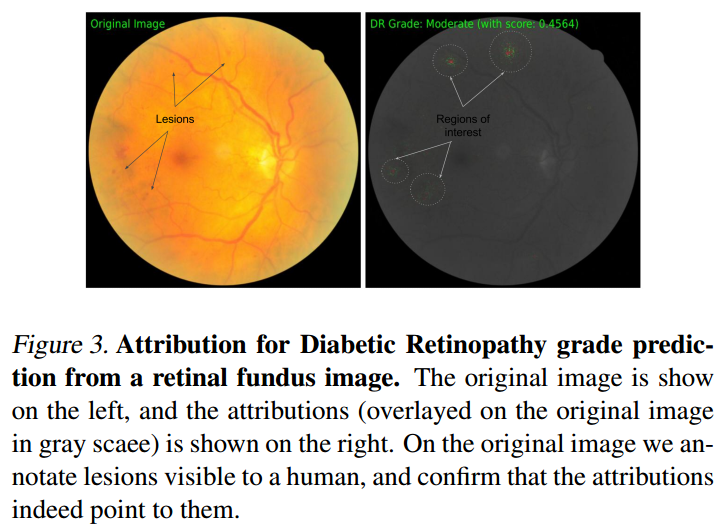
糖尿病视网膜病变预测
使用的模型是【Gulshan et al., 2016】中提出的,baseline依然是black image,结果如下所示:
问题分类
这里处理的模型是预测我们想要的问题的答案是哪个类型。比如:我们想要的答案是yes/no、或者是时间等等。这里使用的模型是【Kim, 2014】的模型,其训练在WikiTableQuestions数据集【Pasupat & Liang, 2015】上。这里使用的baseline是zero embedding vector。
下面的结果显示,Integrated Gradients确实找到了那个关键词。

机器翻译
使用的模型是LSTM-based Neural Machine Translation System【Wu et al., 2016】。baseline是zero embedding vector。结果如下所示:

化学模型
该模型基于分子GNN架构【Kearnes et al., 2016】,能够针对给定的分子预测是否激活了特定靶点(蛋白、酶)。
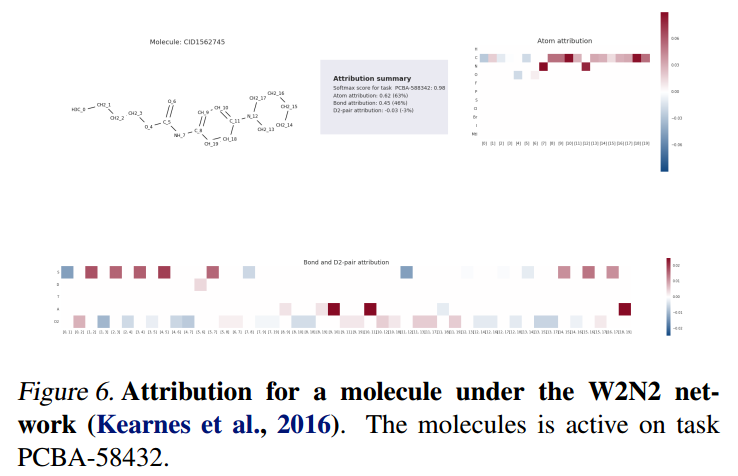
模型显示出有化学键相连的原子贡献了46%,而没有键相连的只贡献了3%。
识别退化特征
将Integrated Gradients方法应用到了W1N2模型【Kearnes et al., 2016】上,发现了其模型中不合理的地方。



